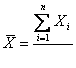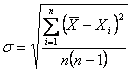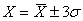| Контроль качества растровых элементов при изготовлении фотоформ |
|
Страница 1 из 2 Цель работы Ознакомление с техникой и метрологическими аспектами линейных измерений в применении к практике полиграфического производства. Получение навыков в работе с прецизионным средством линейных измерений - с компаратором длин ИЗА - 2. Содержание работы Ознакомиться с методикой измерений линейных объектов на микроскопе -компараторе ИЗА - 2. Измерить размеры растровых элементов и пробельных полей на фотоформах и на негативах-копиях, сделанных с фотоформ. На основе результатов измерений и анализа погрешностей измерений следует сделать вывод о влиянии искажений при репродуцировании на качество воспроизведения фотоформ. Теоретическое обоснование Стандартная растровая фотоформа, например, Syntex Test Scale представляет собой совокупность чередующихся с определенной периодичностью системы квадратных или круглых "абсолютно черных" и "абсолютно светлых" элементов (Рис. 1).
Число таких элементов на единицу длины или на единицу площади определяется линеатурой растра. При аттестации какого-либо элемента фотоформы указывается относительное значение площади темных полей к единице площади элемента фотоформ. Например, индекс 40% у элемента фотоформы означает, что темные поля составляют 0.4 от площади элемента и, соответственно 0.6 площади занимают светлые поля. Оптическая плотность элемента фотоформы в соответствии с определением для пучка света, заполняющего весь элемент фотоформы, оказывается равной
Аналогичным образом находится оптическая плотность любого другого элемента стандартной растровой шкалы, поскольку по определению оптической плотности
где S - относительная площадь темных полей, указанная на шкале. Формулы 1 и 2 являются идеальным приближением и дают хорошие результаты при линеатуре растра до 25 линий/см, поскольку они получены при целом ряде допущений:
Невыполнение каждого из этих допущений может привести к снижению качества всех дальнейших технологических операций, выполняемых на допечатной и печатной стадиях полиграфического процесса. На практике в равенство (2) вводятся эмпирические поправки в соответствии с формулой, называемой формулой Юла - Нильсена, т. е.
где Dn - оптическая плотность темного поля, Dном - оптическая плотность прозрачной или непрозрачной копии, изготовленной с данной шкалы, S - относительная затемненная площадь, равная 0 на светлом поле и равная 1 на темном поле, n - эмпирический коэффициент, учитывающий все перечисленные причины отступлений параметров фотоформы от идеальных. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
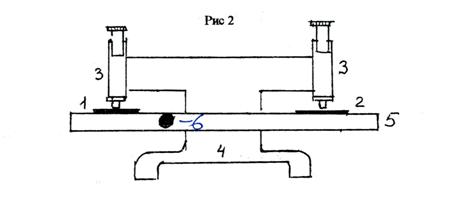
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение Измерения координат темных полей растровых точек стандартных шкал на компараторе ИЗА-2 Размеры растровых точек в данной работе необходимо измерить на компараторе длин ИЗА-2, позволяющем измерять линейные размеры с точностью до 0.0003 мм (или 0.3 мкм). Компаратор длин представляет собой жестко соединённую пару микроскопов, один из которых наводится на какую – либо часть измеряемого объекта, а во второй наблюдается прозрачная шкала с миллиметровыми делениями (рис. 2).
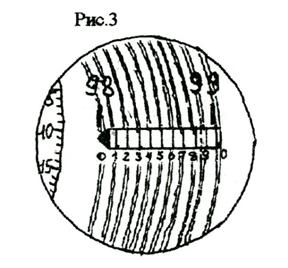
Принцип измерения состоит в сравнении (компарировании) координаты объекта, на который наведены риски измерительного микроскопа, с координатами прецизионной стеклянной линейки. Линейные размеры по одной координате находятся как разность отсчетов начальной и конечной точек измеряемого объекта: L = X1 - X2 где X1 и X2 - координаты правого и левого краев растровой точки, измеренной на микроскопе. Для достижения высокой точности измерения в микроскопе – компараторе ИЗА-2 установлено устройство, называемое окулярный микрометр со спиралью Архимеда. Это устройство сочетает в себе преимущества нониуса к микрометрического винта одновременно. Принцип действия поясняется рисунком 3, где показана шкала измерительного микроскопа, видимая в окуляр.
В поле зрения микроскопа помещена визирная сетка с прямолинейной шкалой, разделенной на 10 делений - нониус. На эту неподвижную шкалу наложена другая стеклянная шкала, на которую нанесена спираль Архимеда с шагом, равным цене деления прямолинейной шкалы (0,1 мм). Соответственно, шаг спирали Архимеда, равный полному обороту лимба спирали, можно разделить на более мелкие деления, чем 0,1 мм. В компараторе ИЗА-2 лимб разделен да 100 делений. Шкала лимба наблюдается в правом (измерительном) микроскопе в левом верхнем углу поля зрения. Таким образом отсчет координаты может быть проведен по шкале лимба с точностью 0,1 мм/100 т.е. 0,001 мм. Кроме того визуально оператор может оценить часть деления лимба по крайней мере с погрешностью не более, чем в 1/3 цены деления. Из совокупности значений координаты, считанной с миллиметровой линейки, с нониуса, с лимба, погрешность измерения координаты тачки, на которую наведен левый микроскоп компаратора ИЗА-2 составляет 0,0003 мм или 0,3 мм. Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе При измерения - снятии отсчета координаты - пластинка со спиралью поворачивается вокруг центра спирали. Начало круговой шкалы (отсчет 0) соответствует тому положению спирали, когда каждый из ее витков совпадает с соответствующей риской прямоугольной шкалы (число витков спирали равно числу делений прямоугольной шкалы). Витки спирали делают двойными, так как это облегчает совмещение риски миллиметровой шкалы с серединой между двумя линиями спирали Архимеда. В измерительный микроскоп наблюдается одновременно три шкалы:
Для того, чтобы измерить координату точки объекта, необходимо вращать спираль Архимеда до совпадения ее витка с штрихом миллиметровой шкалы Тогда целое число миллиметров будет равно меньшему значению из тех, между которыми попал нуль прямоугольной шкалы. Десятые доли миллиметра считываются о прямоугольной шкалы - также меньшее из двух значений среди которых находится штрих миллиметровой шкалы. Сотые и тысячные доли миллиметра считываются с круговой шкалы. Десятитысячные доли миллиметра оцениваются на глаз как дали деления круговой шкалы. Это можно сделать с погрешностью не хуже 1/3 целого деления, т.е. 0,0003 мм. Окончательно координата точки определяется как
где A - отсчет по подвижной миллиметровой шкале, B - отсчет по прямоугольной шкале, десятые доли миллиметра, C - отсчет по круговой шкале, сотые и тысячные доли миллиметра, D - опенка доли деления на круговой шкале, десятитысячные доли миллиметра При измерении на компараторе ИЗА-2 возможны следующие погрешности:
Погрешности пп 1-2 являются систематическими и минимизации накоплением статистических данных не поддаются. Погрешности пп 3,4,5 носят случайный характер и могут быть оценены проведением серии измерений с дальнейшей обработкой по распределению Стыодента для ограниченного числа измерений с нормальным распределением результатов. В данной работе следует координату каждой точки определять по трем независимым измерениям. За истинное значение нужно принимать среднее арифметическое из результатов трех измерений:
По этим же измерениям нужно вычислить среднеквадратическое отклонение, равное:
где n=3 - число независимых измерений Погрешность полученного результата будет составлять значение с доверительной вероятностью 0,9. Окончательно, результат измерения координаты края непрозрачного элемента растровой шкалы будет равен;
|



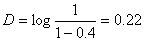
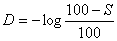
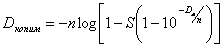
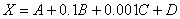
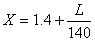 , где L - измеряемая длина в мм. При измерении малых длин (меньших 1 мм) эту погрешность можно не учитывать.
, где L - измеряемая длина в мм. При измерении малых длин (меньших 1 мм) эту погрешность можно не учитывать.