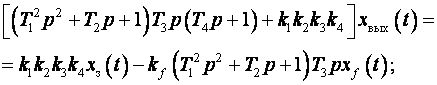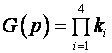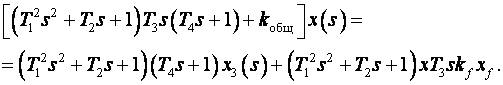| Исследование характеристик систем автоматического управления и их элементов с помощью ПЭВМ |
|
Страница 1 из 2 Исследование динамических характеристик элементов систем автоматического управления (САУ) Независимо от конкретного исполнения и функционального назначения элементы САУ при исследовании ее динамики представляются в виде динамических звеньев. Под динамическим звеном понимается математическая модель элемента, объекта или части системы. Если звено представляется дифференциальным уравнением не выше второго порядка, оно называется элементарным: T12 Из этого уравнения можно получить ряд более простых уравнений, которые характеризуют типовые элементарные динамические звенья: безынерционное, инерционные 1-го и 2-го порядка, колебательное, интегрирующее, дифференцирующее. Сложное динамическое звено представляет собой совокупность элементарных звеньев. Автоматическая система, включающая в себя бесчисленное множество элементов и объектов, может быть представлена конечным небольшим числом динамических звеньев. Динамическая характеристика связана с понятием переходного процесса и определяется передаточной функцией, частотной передаточной функцией и переходной функцией. Передаточной функцией называется отношение изображений по Лапласу выходного и входного воздействий с нулевыми начальными условиями:
Частотной передаточной функцией называется отношение изображений по Фурье выходного и входного воздействий с нулевыми начальными условиями:
Амплитудная частотная характеристика Фазовая частотная характеристика , Для анализа элементов САУ строится годограф частной передаточной функции (амплитудно-фазовая частотная характеристика) – геометрическое место точек концов вектора Переходная функция – это функциональная зависимость выходного воздействия от времени при подаче на вход ступенчатой единичной функции 1 с нулевыми начальными условиями. Типовые динамические звенья Безынерционное звено Безынерционным (усилительным) называется звено, характеризуемое и в статике, и в динамике алгебраическим уравнением:
Передаточная функция звена
Частотная передаточная функция
Рис. 1.1 Частотные характеристики и переходная функция безынерционного звена Инерционное звено первого порядка
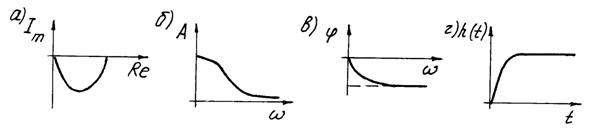
Передаточная функция и частотная передаточная функция (рис. 1.2, а)
Амплитудная и фазовая частотные характеристики (рис. 1.2, б, в)
Переходная функция (рис. 1.2, г)
Рис. 1.2 Частотные характеристики и переходная функция инерционного звена первого порядка Инерционное звено второго порядка
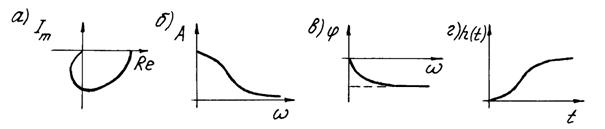
Передаточная функция и частотная передаточная функция (рис. 1.3, а)
Рис. 1.3 Частотные характеристики и переходная функция инерционного звена второго порядка Амплитудная и фазовая частотные характеристики (рис. 1.3, б, в)
Переходная функция, согласно корням характеристического уравнения T12p2 + T2p + 1 = 0
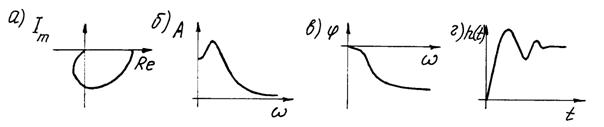
Колебательное звено
при условии: T22 – 4T12 < 0. Рис. 1.4 Частотные характеристики и переходная функция колебательного звена Интегрирующее звено
Передаточная функция и частотная передаточная функция Амплитудная и фазовая частотные характеристики Переходная функция h(t) =
Рис. 1.5 Частотные характеристики и переходная функция интегрирующего звена Дифференцирующее звено
Характеристики звена:
Рис. 1.6 Частотные характеристики и переходная функция дифференцирующего звена Исследование динамических характеристик типовых звеньев САР можно провести аналитически с учетом фактических значений параметров K и i или с использованием специальных программ (см. комплекс “Avtomat”). Для исследования динамических характеристик элементов и объектов САУ необходимо получить численные значения параметров динамических звеньев – коэффициента передачи К (статический параметр) и постоянной времени Т (динамический параметр). Коэффициент передачи можно получить из графика статической характеристики элемента, найденной либо аналитически на основании использования физического закона, описывающего реальный процесс, протекающий в элементе, либо экспериментально. Постоянную времени можно определить расчетным путем или путем выбора приведенных в справочных таблицах значений (как правило, принимаются средние значения). Исследование динамических характеристик САУ Передаточные функции автоматических систем При анализе автоматической системы рассматриваются передаточные функции, относящиеся к самой системе. Передаточная функция разомкнутой системы
Передаточная функция замкнутой системы определяется по соответствующему входу. По заданному воздействию
по возмущению Частотная передаточная функция САУ Частотная передаточная функция САУ получается из передаточной функции системы заменой S на iw:
Переходный процесс САУ Переходный процесс может быть вызван двумя причинами: начальным отклонением координат состояния системы и появлением внешнего входного воздействия. Это собственные движения в системе. Для построения переходного процесса необходимо получить математическую модель САУ. Исходные дифференциальные уравнения системы составляются двумя методами: общим и с помощью передаточных функций. Первый метод основан на имеющихся дифференциальных уравнениях элементов системы, записанных в операционной форме. Составляется система уравнений, которая разрешается относительно Xвых:
где Систему уравнений можно разрешить относительно ошибки, тогда
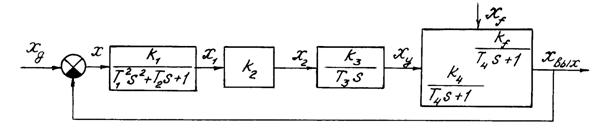
Допустим, САУ представлена структурной схемой (рис. 2.1).
Рис. 2.1 Структурная схема САУ Система дифференциальных уравнений:
Использовав метод подстановки, разрешим систему уравнений относительно Xвых:
D(p) = a0 p4 + a1 p3 + a2 p2 +a3 p + a4;
N(p) = c0 p3 + c1 p2 + c2 p. Аналогично можно разрешить систему уравнений относительно ошибки x. Второй метод основан на передаточных функциях системы. Необходимо получить передаточную функцию разомкнутой системы
где k1, k2, k3, k4 = kобщ k1 k2 k3 k4 = kобщ. Передаточная функция управляемого объекта по возмущению
Подставив эти выражения в уравнение, разрешенное относительно ошибки, получим:
Аналогично составляем уравнения относительно Xвых:
Динамические характеристики САР можно получить аналитически с учетом фактических значений параметров всех звеньев или с использованием специальных программ (см. комплекс “Avtomat”). Устойчивость САУ Устойчивость системы – это ее свойство возвращаться в состояние установившегося равновесия после снятия возмущения, нарушившего это равновесие. Устойчивость – необходимое условие для автоматической системы: Прямой способ исследования устойчивости системы заключается в нахождении решения однородного дифференциального уравнения. Переходные процессы носят затухающий характер. Для упрощения анализа устойчивости находят корни характеристического полинома D(s)=0 . Система является устойчивой, если все вещественные корни и действительные части комплексных корней отрицательны. Аналитическое нахождение корней полинома возможно до третьего порядка (включительно), а при порядке более третьего используют средства вычислительной техники (см. комплекс “Avtomat”). Широко распространен метод Найквиста для проверки устойчивости САР. Система устойчива, если годограф частотной характеристики разомкнутой системы не охватывает точку с координатами (-1,0i) . Этот метод реализован в программном комплексе “Avtomat”.
|


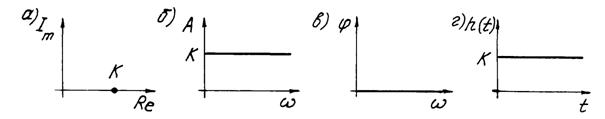
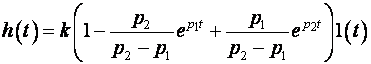 .
.
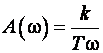 ;
; 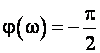 .
.