В лабораторной работе исследуются интерполяционные алгоритмы,используемыев программе Photoshopи алгоритм билинейной интерполяции, реализованный на вычислительной базе программы. Все опыты проводятся начерно-белых экранных изображениях. Работа интерполяционных алгоритмов исследуется научастках изображения с изменяющимися значениями сигнала:

• резкий контур, разделяющий протяженные участки изображения двух значений тона полного контраста и неполного контраста;
• размытый контур, разделяющий протяженные участки изображения двух значений тона полного и неполного контраста;
• одиночные штрихи шириной от одного элемента пространственной дискретизации полного и неполного контраста;
• миры с пространственными частотами от максимальной и ниже полного и неполного контраста;

На начальном этапеисследованиярекомендуетсяиспользоватьизображения с вертикальными (горизонтальными) прямолинейными контурами и активизировать алгоритмы интерполяциипо одной пространственнойпеременной, например, применяя одномерное масштабирование изображения. Это позволяет исследовать двухмерные интерполяционные алгоритмы в одномерном виде. Для получения контуров различной пространственной ориентациирекомендуется использовать изображения знаков шрифта неполного контраста с “мягким” контуром (Рис.6) или “жестким” контуром (Рис.7). Приведенные на рисунках примеры имеют размер 100 на 100 элементов пространственной дискретизации (пиксел).

Рис. 6

Рис. 7

Все изображения сохраняются в виде графических файлов и используютсяпри защите лабораторной работы.Результаты оцениваются методом визуального сравненияисходных и преобразованных изображений по критерию графической точности и методом измерениячисленных характеристик контуров, в т. ч. их частотно пространственных характеристик, с использованием метрологическихсредств программного пакета Photoshop и методом построения графиков в программе. Нарис.8 показан результат двойного масштабирования исходного изображения (Рис.7) с масштабом 50% и масштабом 200% при бикубической интерполяции. Сравнение полученногов результате двух масштабных преобразований изображения с исходным позволяет оценить графические потери при бикубической интерполяции. Аналогичные преобразования, проведенные для всех видов интерполяции, позволяют сравнить интерполяционные алгоритмы по критерию графических потерь.

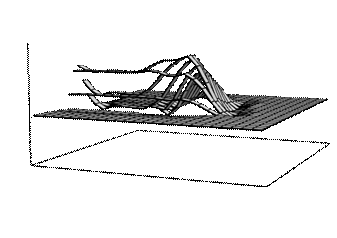
Рис. 8

По выделенной на рис.8 области размером 25 на 25 элементов в программе построен график (Рис.9), на котором результат работы алгоритма бикубической интерполяции представлен зоной размытия контура, значения сигнала в которой образуют кубическую параболу.

Рис. 9

Применение программы Excel, непосредственно не предназначенной для обработки изображений, требует некоторых ограничений и преобразований исходного файла. Для обработки в программе могут быть использованы цифровые изображения или их фрагменты квадратной формы размером не более 256 на 256 элементов пространственной дискретизации. Ограничения размера связаны с максимальным числом столбцов таблицы (256), которая может быть обработана в программе Excel.Квадратная форма изображений принята для упрощения процедуры согласования графического файла формата *.raw и программы. Программа предназначена для обработки числовых массивов, представленных в текстовой кодировке ASCII. Для конвертирования значений цифрового сигнала тона из прямого двоичного кода в код ASCIIиспользуется программаbintxt .exe, исходный текст которой на Turbo Pascal приведен ниже.

program BINTXT;

var

y:byte;

x,a,r:word;

f1: file of byte;

f2:text;

z,h,d,v,b:string;

k:boolean;

const

m='\';

label

op, op1, op2, op3;

begin

getdir(0, z);

write('Ввести имя исходного файла', #13, #10);

readln(h);

d:=(z + m) + h;

write('Ввести имя конечного файла',#13,#10);

readln(b);

v:=(z + m) + b;

assign(f1, d);

assign(f2, v);

reset(f1);

rewrite(f2);

a:=filesize(f1);

x:= round(sqrt(a));

r:=0;

a:=x;

op: seek(f1, r);

k:=eof(f1);

if k=false then goto op2 else goto op1;

op2: read(f1, y);

if y<100 then write(f2,#32);

if y<10 then write(f2,#32);

write(f2,y);

r:=r+1;

if a=1 thengoto op3 else write(f2,#32);

a:=a-1;

goto op;

op3: write(f2,#13,#10);

a:=x;

goto op;

op1: close(f1); close(f2);

end.

На примере изображений текстур из точек минимального размера может быть промоделирован процесс повторной дискретизации с увеличением интервала. Как указывалось выше, любая дискретизация, в т.ч. повторная, требует ограничения пространственного спектра в соответствии с выбранной частотой дискретизации. В приведенных на рис.10 и рис.11 примере повторной дискретизации использовалась ступенчатая интерполяция при изменении числа интервалов от до , т. е. при масштабировании цифрового изображения с масштабом 10% за счет изменения числа элементов в матрице двухмерного сигнала. Для получения исходного физического размера изображения интервал дискретизациипромасштабирован с масштабом 1000%. В результате за счет транспонирования не ограниченного нанужном уровне спектра исходного сигнала в область низких частот элементы текстуры стали более различимы. Аналогичный эффект возникает при сканировании оригинала с интервалом сканирования, значительно превышающим размер апертуры.

Рис. 10

Рис. 11

С помощью программы Excel моделируется алгоритмлинейной интерполяции по строке изображения. Программавыбрана как наиболее простое и доступное средство вычислений, позволяющее выполнять расчеты для двухмерных цифровых массивов данных, представляющих цифровые изображения. В лабораторной работе моделируется одномерный вариант билинейного алгоритма интерполяции в пределах только одной, произвольно выбранной строки (см. файл qnep.xls). Расширение возможностей алгоритма на все строки изображения и на полный двухмерный вариант приводит к чисто количественному усложнению.

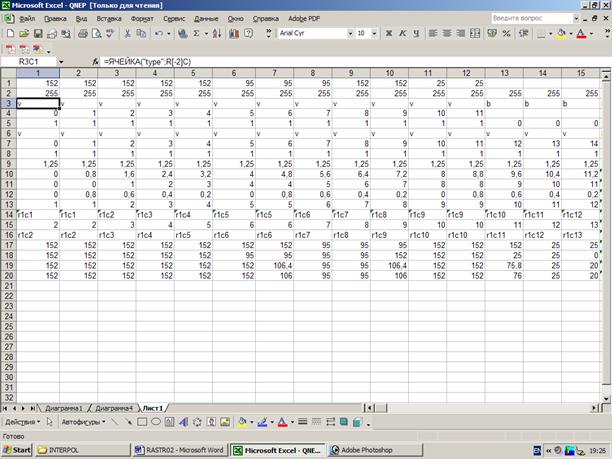
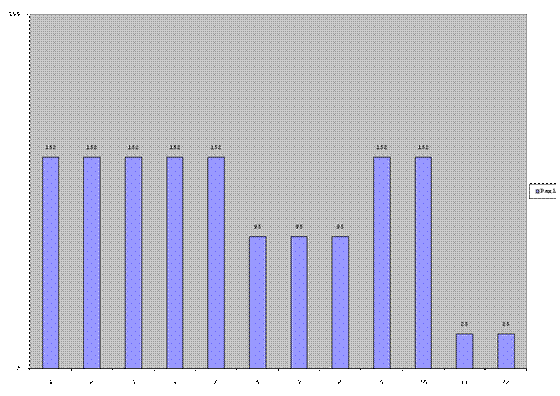
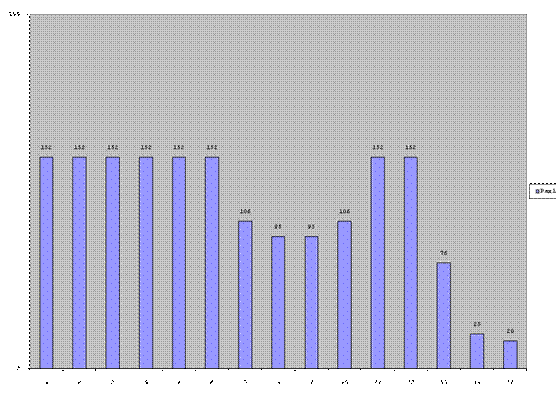
Пример реализации алгоритма линейной интерполяции в программе Excel для одной строки произвольного изображенияприведен на рис.12. Первая строкатаблицы используется для ввода цифровых значений сигнала строки исходного изображения. Ввод значений в пределах одного байта (0-255) может выполняться вручную, что позволяет исследовать работу алгоритма линейной интерполяции для различных вариантов изменения входных сигналов от пространственной переменной.При вводе произвольной строки изреального цифрового изображения, преобразованного в текстовый формат программой bintxt .exe (см. выше), число значений цифрового сигнала на превышает255. В приведенном на рис.12 примере длина исходной строки составляет 12 элементов пространственной дискретизации. На рис.13 показана гистограмма исходной строки.

Рис. 12

Вторая строка таблицы (см. рис.12) используетсядля задания длины строкицифрового изображения после масштабирования. В приведенном на рис.12 примере длина строки после масштабирования выбрана 15 элементов дискретизации, что дает коэффициент масштабирования или 1,25 (125%).

Последняя (20-я) строка таблицы – это результат работы алгоритма, формирующего значения перевыборки строки изображения после масштабирования с линейной интерполяцией. По этим значениям построенагистограммы на рис.14.Последнее (15-е) значение в строке рассчитывается с ошибкой, вызванной краевым эффектом.

Каждая строка таблицы(см. рис. 12) выполняет одну из функций программы , кроме первых двух, с помощью которых задаются значения исходных сигналов и параметры преобразования.

Рис. 13

Рис. 14

Задания

1. Изучить принцип двухмерной интерполяции для одномерных и двухмерных сигналов;
2. Изучить озможности программы Photoshop в части интерполяционныхалгоритмов;
3. В программе Photoshop подготовить тестовые изображения,пригодные для исследования интерполяционныхалгоритмов на контурах разного типа (могут быть использованы как одиночные так комплексные тесты);
4. Для подготовленных тестовых изображений провести сравнительный анализ трех вариантов интерполяции, предусмотренных в программе Photoshop в одномерном и двухмерном виде;
5. Выполнить масштабирование изображения двумя методами;
6. Исследовать несколько (два или более) вариантов линейных пространственных преобразований, предусмотренных в программе Photoshop, приводящих к необходимости интерполяции;
7. Результаты интерполяции (наиболее характерные) представить в виде трехмерных и двухмерных (в пределах строки изображения) графиков в программе Exel
8. Провести измерения пространственно частотных характеристик изображений до и после интерполяции, используя в качестве измерительных средств пространственные фильтры и гистограммы программы Photoshop;
9. Исследовать действие алгоритма линейной интерполяции с помощью модели в программe.

Контрольные вопросы

1. Повторная дискретизация или перевыборка;
2. Ступенчатая интерполяция;
3. Линейная интерполяция
4. Общий принцип двухмерной интерполяции;
5. Алгоритм определения опорных отсчетов при билинейной интерполяции;
6. Алгоритм расчета интерполяционного значения при билинейной интерполяции;
7. Принципы масштабирования изображения, представленного в растровом виде;
8. Зависимость результата интерполяции от степени интерполяционного полинома;
9. Зависимость результата интерполяции от шкалы квантования базовых значений сигнала:
10. Принцип измерения пространственно частотных характеристик изображения в программе Photoshop;
11. Критерии определения резкости;
12. Анализ результатов измерений резкости после интерполяции;
13. Принцип реализации алгоритма билинейной интерполяции в программе.