| Интерполяционные алгоритмы при пространственных преобразованиях изображений |
|
Страница 1 из 2 Принципы интерполяции для двухмерных сигналов Интерполяция – это нахождение значений аналоговой функции однойили нескольких переменных по конечному набору известных (опорных)значений функции.При обработке полиграфических изображений в допечатном процессеинтерполяция используется на следующих основных этапах:
В основе двухмерной интерполяции, применяемой к зображениям, как двухмерным сигналам, лежат принципы одномерной интерполяции. Функция одной переменной
Такой вид интерполяции (1) называется полиномиальной.Функция Задача полиномиальной интерполяции – нахождение коэффициентовинтерполяционного полинома (1)
Приобработке изображений это условие выполняется только для группыпространственных отсчетов, расположенных в непосредственной близостиот восстанавливаемого пространственного интервала. Используемые при интерполяцииполиномы ограничены, как правило, третьей степенью, что связано сограниченным набором значений сигнала, отвечающих указанному условию и усложнениемалгоритма расчета для полиномов более высоких степеней. Усложнениеалгоритма приводит к увеличению времени его выполнения, чтосущественно замедляет процесс обработки изображения в инструментальныхпрограммных средах. Последовательное применение одномерных интерполяций для получениязначения пространственного интерполяционного отсчета сохраняетназвание базовой одномерной интерполяции с приставкой “би”, например,билинейная, бикубическая и т.д.Результат или качество интерполяции проявляется, в основном, на контурахизображения, для которых потеря информации при ограничениипространственного спектра сигнала, например, при сканировании,наиболее значительна. Для полинома нулевой степени характернообразование ступенчатого контура, а для полиномов более высокихстепеней – образование зоны размытия, закон изменения сигнала в которой соответствует используемому полиному. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
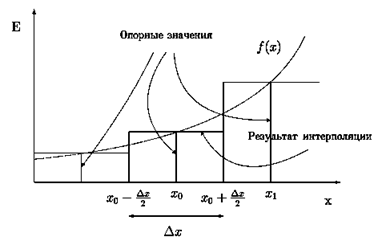
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение Простейший вариант интерполяции соответствует случаю, когдаинтерполяционные значения рассчитываются по единственному опорномузначению для всего интервала интерполяции. Для одномерного сигнала этозначение
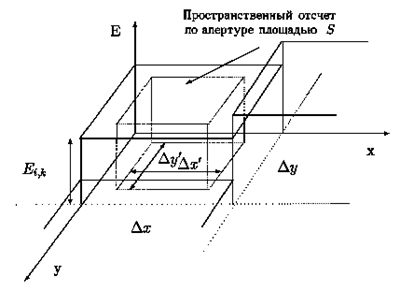
При двухмерной ступенчатой интерполяции каждая ступень представленаплоскостью, ограниченной: апертурой сканирования интервалом пространственной дискретизации При сканировании изображения прямоугольной апертурой
Эта операция, имеющая смысл ступенчатой интерполяции, формируетединственное значение сигнала-представителя для всего элементапространственной дискретизации при всех возможных соотношениях При обработке цифровых изображений метод ступенчатойинтерполяциииспользуется на всех этапах, требующих цифро-аналогового преобразования,т.е. перехода от цифрового представления элементов изображения в видепрямого двоичного кода
где: Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе Более сложная при технической реализации линейная интерполяциявыполняется по двум опорным отсчетам сигнала:
Для линейной интерполяции используется многочлен первой степени:
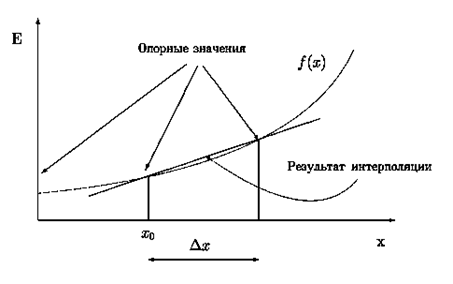
Рис.2 При линейной интерполяции предполагается, что искомая аналоговаяфункция изменяется пропорционально своему аргументу. Линейная интерполяциядает более точный результат, чем ступенчатая, но требует болеесложного алгоритма и большего времени для еговыполнения. На рис.3 показан пример линейной интерполяции дляодномерного сигнала.
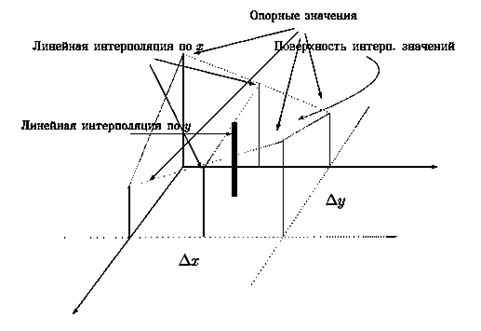
Рис. 3 При обработке двухмерных сигналов применяется билинейная интерполяция, в процессе которой формируются одномерные (линия) идвухмерные (поверхность) аналоговые сигналы (Рис.4), покоторым может быть выполнена повторная пространственная дискретизация(перевыборка).
Рис.4 Интерполяция при масштабировании цифрового растрового изображения В общем виде цифровое растровое изображение может быть представлено двумяматрицами одинакового размера: 1) Матрицей дискретных значений сигналов, упорядоченных по строкам истолбцам по их реальному положению в границахизображения:
2) Матрицей координат, соответствующих отсчетам пространственнойдискретизации с постоянными интервалами
где: Задача масштабирования в растровой графике может быть решенаумножением матрицы координат на скалярный коэффициент масштабирования
в результате чего образуется новая матрица (7), равная по размеру исходной матрице (6):
где: Матрица (7) остается равновеликой сматрицей (6) и каждому пространственному отсчетуновой матрицы соответствует значение сигнала. Размер изображения в данном случаеизменяетсяза счет масштабирования интервала пространственнойдискретизации при сохранении числа элементов матрицы
где: Данный метод масштабирования является также основным для телевидения,цифровых камер и для всехграфических систем, где количество элементов изображения (пиксел)фиксировано и не зависит от размера изображения. Другой метод масштабирования применяется для полученияпроизвольного масштаба при сохранении интервала пространственнойдискретизации. Этот методоснован на изменении размера матрицыкоординат: После преобразования матрица координат принимает вид:
где: Матрица значений сигнала (5) приводится в соответствие с матрицей координат (9) методом интерполяции. Рассмотрим процесс интерполяции в одномерном виде в пределахстроки матрицы координат и строки матрицы значений сигнала.Длина строки пространственно дискретизированного изображения домасштабирования
При умножении числа элементов строки на масштабный коэффициент
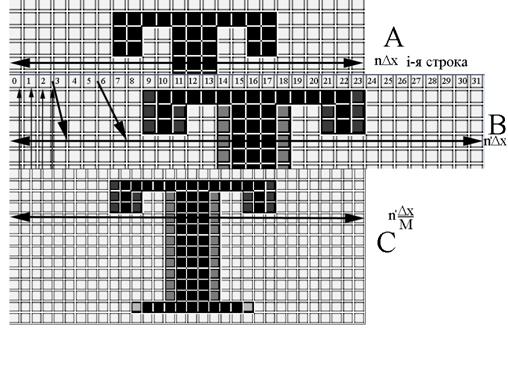
Рис.5 На рис.5 показан принцип одномерного масштабирования растровогоизображения по координате x с коэффициентом Для примера рассмотрен алгоритм билинейной интерполяции, позволяющий получить достаточную точностьрасчетапри обработкеизображений в реальном времени, например, при их сканировании.Принцип построения алгоритма рассматривается для одномерного варианта (по координате x)в соответствии с рис.5 и обобщается на двухмерный вариант. При выполнении интерполяционных расчетов необходимо разделять понятие опорного значения сигнала для пространственного отсчета, как точки, для которой удовлетворяется условие дискретизации по двум пространственным переменным Алгоритм решает две задачи:определение индексов интервала опорных значений, покоторым выполняется расчет каждого значения перевыборкиисобственно расчет интерполяционного значения сигналапо положению отсчета перевыборкивинтервале. Определение взаимного расположения опорных отсчетов и отсчетов перевыборки В зависимости от значениякоэффициента масштабирования часть отсчетов перевыборки можетсовпадать с опорными значениями. Для данногопримера каждое третье опорное значение совпадает с каждым четвертымотсчетом перевыборки (Рис.5). При любоммасштабе нулевой опорный отсчет каждой строки совпадает с нулевымотсчетом перевыборки. Первая задача алгоритма – определить пары опорных отсчетов, по которымбудет выполнена линейная одномерная интерполяция для данного отсчетаперевыборки. Для решения этойзадачи можно использовать следующую очередность операций: Текущий номер отсчета перевыборки В полученном результате выделяется целая часть В значении Аналогичныедействия выполняются для отсчета перевыборки попространственной переменной Расчет интерполяционных значений Для решения второй задачи, т.е. собственно расчета значениясигнала перевыборки
где: Аналогично выражению (13) может быть получено выражение для второго значения линейнойодномерной интерполяции по
По полученной из выражений (13) и (14) паре значений
Выражение (15) является аналитической основой для алгоритмаопределения значения перевыборки по найденным в первой части алгоритмачетырем опорным значениям и относительным смещениям Значение сигнала для пространственного отсчета перевыборки равносумме значений окружающих опорных отсчетов, умноженных на весовыекоэффициенты, показывающие относительную пространственную близость котсчету перевыборки. Максимальное значение весового коэффициента – единица, и в этом случае отсчет перевыборки пространственно совпадает ссоответствующим опорным отсчетом и принимает его значение.
|



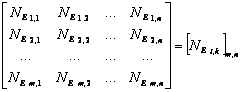

 ,
,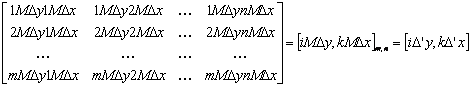
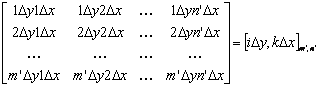
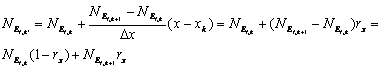 (13)
(13)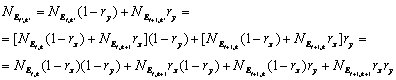 (15)
(15)