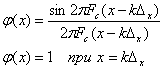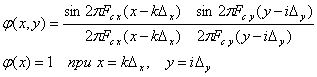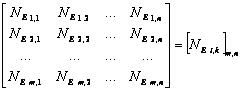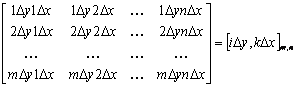| Сканер |
|
Страница 1 из 6 Общие положения Классификация изображений и средств их ввода в полиграфическую технологию Значительная доля исходной информации в полиграфической технологии представлена в форме изображений на вещественных носителях. Их принято разделять на две категории:
К первой категории относятся изображения на бумаге, фотобумаге и других материалах с подобными оптическими свойствами, воспринимаемые зрением как двухмерные сигналы яркости за счет отражения света стороннего источника. В полиграфии эти изображения принято относить к полностью непрозрачным и для их представления использовать только два оптических коэффициента: - коэффициент отражения и - коэффициент поглощения. Третий реально существующий оптический коэффициент - коэффициент пропускания принимается равным нулю. Непрозрачные изображения, используемые как полиграфические оригиналы, относятся к четырем основным группам:
Существенное место занимают также т.н. вторичные оригиналы в виде полиграфических оттисков. При их использовании возникают специфические проблемы, связанные с их растровой структурой. Эти изображения относят к отдельной группе микроштриховых. Ко второй категории относятся изображения на прозрачной основе, для представления которых в виде двухмерного сигнала также используется только два оптических коэффициента - коэффициент пропускания и коэффициент поглощения . Третий оптический коэффициент - коэффициент отражения принимается равным нулю. Прозрачные изображения, используемые как полиграфические оригиналы, относятся к тем же четырем основным группам:
Этап ввода исходного изображения - это переход от двухмерного аналогового сигнала вещественного типа к цифровому одномерному сигналу, пригодному для компьютерной обработки. Для полиграфической технологии операция ввода выполняется с помощью цифровых камер и сканеров. Основная операция, выполняемая при вводе изображения в полиграфическую технологию - это аналого-цифровое преобразование. Преобразование аналогового сигнала в цифровой состоит в отображении несчетного множества значений аналогового сигнала в конечное множество, образующее цифровой сигнал. В общем виде эта процедура может быть представлена как разбиение векторного пространства аналоговых сигналов на конечное множество подпространств, для каждого из которых выбирается один принадлежащий ему представитель. Все остальное (бесконечное) множество значений сигнала каждого подпространства заменяется этим сигналом-представителем. Подпространствам присваиваются численные идентификаторы, и каждому аналоговому сигналу может быть поставлено в соответствие число - номер сигнала-представителя. Рассмотренная процедура называется обобщенным квантованием. Основа обобщенного квантования - это выбор метрики, т.е. способа измерения отличия значений сигналов друг от друга, и выбор величины отличия сигналов от их представителей в пределах каждого подпространства на основе допустимой погрешности. И метрика и сами величины подпространств определяются требованиями к точности цифрового представления, т.е. согласуются с параметрами получателя информации. Реализовать процедуру обобщенного квантования на техническом уровне, как правило, невозможно. Основная причина в многомерности векторных пространств сигналов и в сложности выбора метрики. Эти сложности особенно проявляются при преобразовании в цифровую форму цветных изображений. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение На практике используется двухступенчатая процедура, состоящая из дискретизации двухмерного сигнала по пространственным переменным и поэлементного квантования дискретных значений. Операции дискретизации и квантования изображения, как двухмерного аналогового сигнала, выполняются элементами сканера. Как и все операции обработки и преобразования сигналов, дискретизация и квантование выполняются с их математическими моделями - функциями одной или нескольких переменных. Монохромное изображение как двухмерный сигнал может быть представлено функцией двух пространственных переменных . Значение функции - это оптический (световой) параметр: оптическая плотность, оптический коэффициент, яркость, светлота. Пространственные переменные - это текущие координаты точки на плоскости в пределах формата изображения . Трехкомпонентной моделью цветного изображения является система из трех функций двух пространственных переменных. Для трехкомпонентной аддитивной системы RGB, являющейся базовой при сканировании и выводе на экран цветных изображений, система функций примет вид: Значения функций пропорциональны яркости или светлоте для красной, зеленой и синей базовых составляющих аддитивной RGB цветовой системы. Преобразования сигнала, в т.ч. квантование и дискретизация, выполняются по каждой функции в отдельности. Сервис онлайн-записи на собственном Telegram-боте
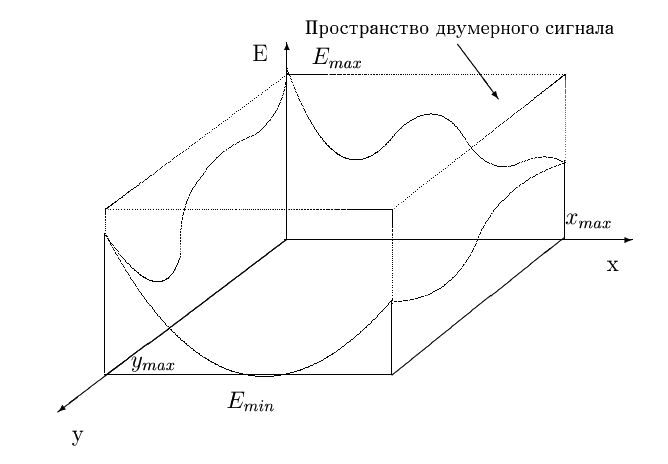
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе Функция двух пространственных переменных может быть представлена графически в виде поверхности, высота каждой точки которой над плоскостью (ордината) соответствует значению параметра для текущей пары координат (Рис. 1).
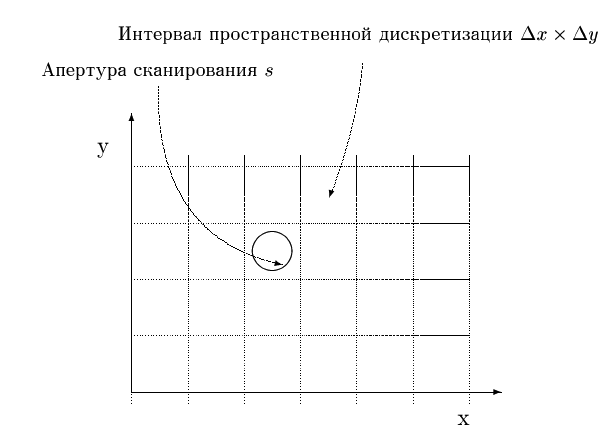
Рис. 1 Одна из главных операций, выполняемых сканером - пространственная дискретизация изображения или собственно операция сканирования. Дискретизация - это замена непрерывного сигнала конечной последовательностью его отдельных значений. Результат дискретизации или качество дискретизации может быть оценено по точности восстановления исходного сигнала по конечному набору дискретных отсчетов - значений решетчатой функции. Точность восстановления, в свою очередь, зависит от основного параметра дискретизации - интервала. Для двумерных сигналов интервал дискретизации - это участок плоскости пространственных переменных, ограниченный прямоугольником (Рис.2).
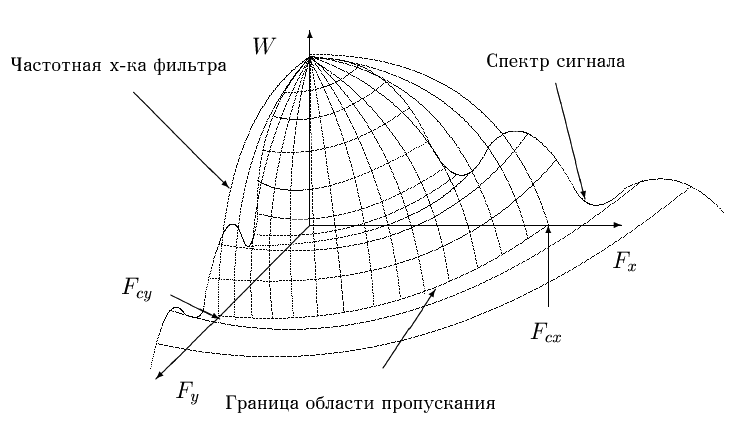
Рис. 2 В большинстве систем используется квадратный интервал дискретизации . Изменение конфигурации интервала пространственной дискретизации, связанное с определенными техническими ограничениями, требует введения дополнительных преобразований, связанных с масштабированием и интерполяцией. Искажение формы интервала дискретизации свойственно, в основном, планшетным сканерам и связано с различием методов формирования интервала дискретизации по пространственным координатам, например, оптический метод по координате и механический метод по координате . Апертура сканирования является низкочастотным пространственным фильтром, частоты среза которого и форма частотной характеристики определяются размерами и конфигурацией апертуры (Рис.3).
Рис. 3 Двухмерный НЧ фильтр - это участок площади изображения, для которого принимается одно значение сигнала - один представитель несчетного множества значений функции , существующих на данной площадке изображения в границах апертуры. В качестве такого представителя берется интеграл от значений оптического параметра по площади апертуры , преобразуемый фотоэлектрическим преобразователем в электрический аналоговый сигнал .
В современных профессиональных сканерах с высоким разрешением размер апертуры сканирования приближается к минимально возможному значению (единицы микрон), соизмеримому с длиной волны видимого диапазона электромагнитных колебаний. При таких условиях форма апертуры не может быть выбрана произвольно и, как правило, приближается к круглой (см. рис.2). Интервал дискретизации определяется исходя из спектрального критерия, основанного на теореме отсчетов (теореме Найквиста-Котельникова): Сигналы, имеющие финитный спектр, ограниченный частотой среза, могут быть полностью восстановлены методом интерполяции по своим дискретным отсчетам, взятым с интервалом дискретизации .
Теорема Котельникова для одномерного сигнала основывается на одномерном варианте функции отсчетов .
Функция отсчетов для двухмерного сигнала образуется перемножением одномерных функций для пространственных переменных.
Теорема Котельникова для двухмерного сигнала принимает вид:
В результате двумерной дискретизации образуется двумерная решетчатая функция, которая в вещественном виде может быть представлена как растровое изображение, а в виде математической модели - как матрица сигналов-представителей:
где: Матрицы отсчетов пространственной дискретизации
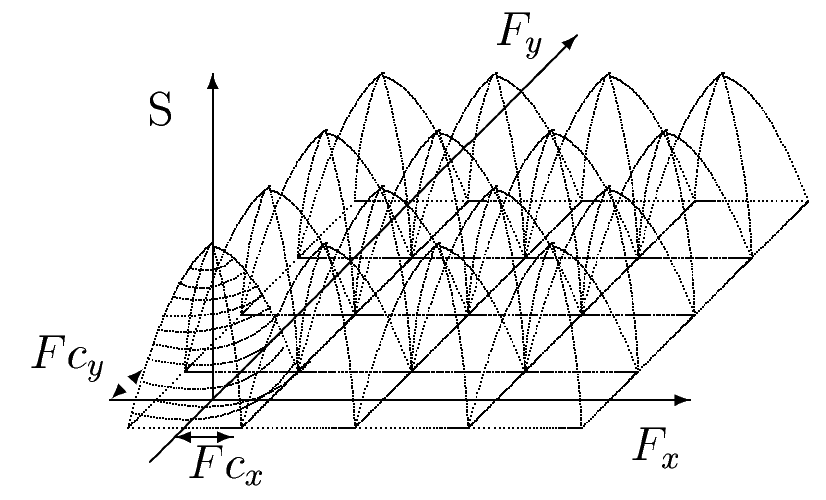
где: n - число элементов в строке изображения (по координате); m - число строк в изображении (по координате). При таком задании матрицы координат закон пространственной дискретизации или процедура сканирования изображения полностью определена интервалом При известных значениях и двухмерная матрица сигнала может быть преобразована в однострочную матрицу или одномерный дискретизированный сигнал. Каждое значение одномерного сигнала имеет свое смещения относительно начала, соответствующее его положению в двумерной матрице. В результате пространственной дискретизации образуется растровое изображение. Каждое сочетание дискретных значений переменных , удовлетворяющее условиям пространственного варианта теоремы Котельникова, заменяется одним числом - порядковым номером данного дискретного отсчета в одномерном массиве. Этот порядковый номер может представлять момент времени при последовательном сканировании изображения или смещение данного отсчета в общем массиве таких же отсчетов, принадлежащих изображению. Основным условием применимости теоремы Котельникова является наличие ограниченного частотами среза спектра сигнала (финитного спектра). При соблюдении этого условия исходный сигнал может быть полностью, без потери информации восстановлен методом интерполяции по своим дискретным отсчетам с сохранением спектральных составляющих до частот среза включительно. Ограничение спектра исходного аналогового сигнала выполняется пространственным фильтром низких частот, по площади которого берется среднее значение сигнала - представителя для всего векторного подпространства в границах интервала дискретизации. Со спектральной точки зрения переход к растровой форме сопровождается потерей части пространственно спектральных составляющих исходного изображения (исходного сигнала) за счет ограничения его спектра и появлением дополнительных спектральных составляющих растра, на котором выполняется пространственная дискретизацмя. Апертура сканирования конечного размера выполняет функцию пространственного фильтра, ограничивающего спектр исходного двухмерного сигнала частотами среза. Результирующий пространственный спектр после дискретизации образуется периодическим повторением ограниченного пространственного спектра сигнала с интервалом повторения, выбранным согласно теореме Котельникова. На рис. 4 показан результирующий спектр после пространственной дискретизации, полученный периодическим повторением ограниченного спектра исходного сигнала. Это идеальный случай дискретизации, при котором спектр исходного сигнала точно равен нулю за пределами области пропускания пространственного низкочастотного фильтра. Для восстановления такого дискретизированного изображения необходимо выполнить операцию двухмерной интерполяции и НЧ фильтрацию с помощью фильтра, пространственно-частотные характеристики которого точно повторяют характеристики входного фильтра, выполнявшего функцию ограничения спектра перед дискретизацией. При таком условии все спектральные составляющие, превышающие значения и являющиеся помехами по отношению к полезному сигналу, будут исключены из результирующего спектра и не будут восприниматься приемником информации (зрением человека).
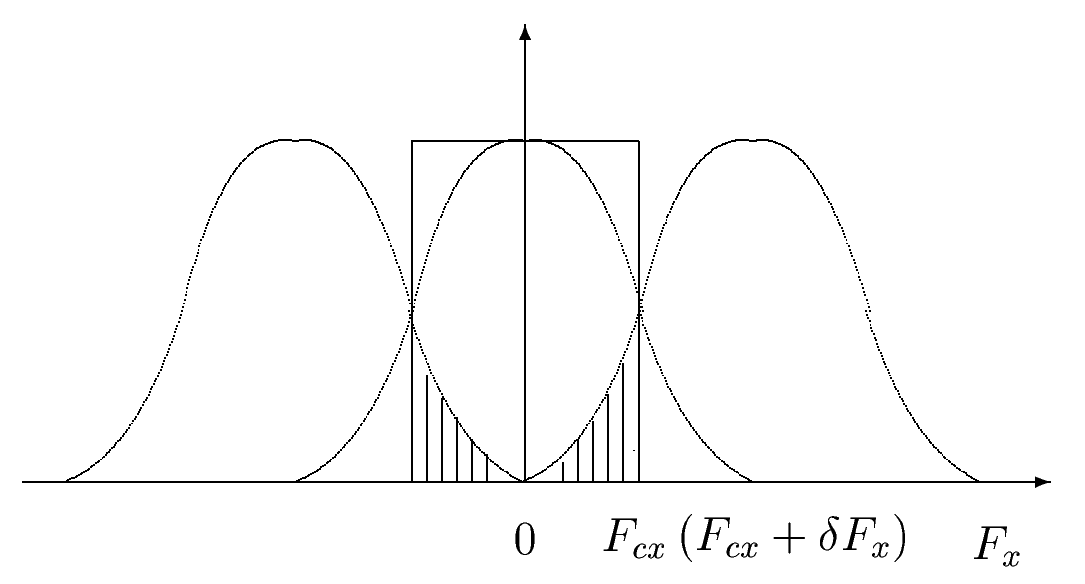
Рис. 4 Получить практически такие условия дискретизации и восстановления сигнала невозможно. Частотная характеристика реального низкочастотного фильтра, представленного, например, сканирующей апертурой, более или менее быстро спадает в пределах некоторого интервала частот, в котором выбирается частота среза - база для применения теоремы Котельникова. На рис.5 представлено сечение по оси частот пространственного спектра дискретизированного изображения при реальной частотной характеристике низкочастотного пространственного фильтра, ограничивающего исходный сигнал.
Рис. 5 Прямоугольником показана частотная характеристики идеального восстанавливающего фильтра и, соответственно, зона спектра сигнала, для которой точно выполняется выбранное условие дискретизации. Частоты, лежащие в интервале При сканировании изображения строб-эффект возникает, когда размер апертуры сканирования существенно меньше интервала пространственной дискретизации (шага сканирования), Значения, получаемые от апертуры сканирования присваиваются всему пространственному интервалу дискретизации. Это приводит к тому, что мелкие дефекты изображения, имеющие, например, характер шума оказываются в области пространственных частот, соответствующих полосе пропускания восстанавливающего фильтра – зрительного аппарата человека.
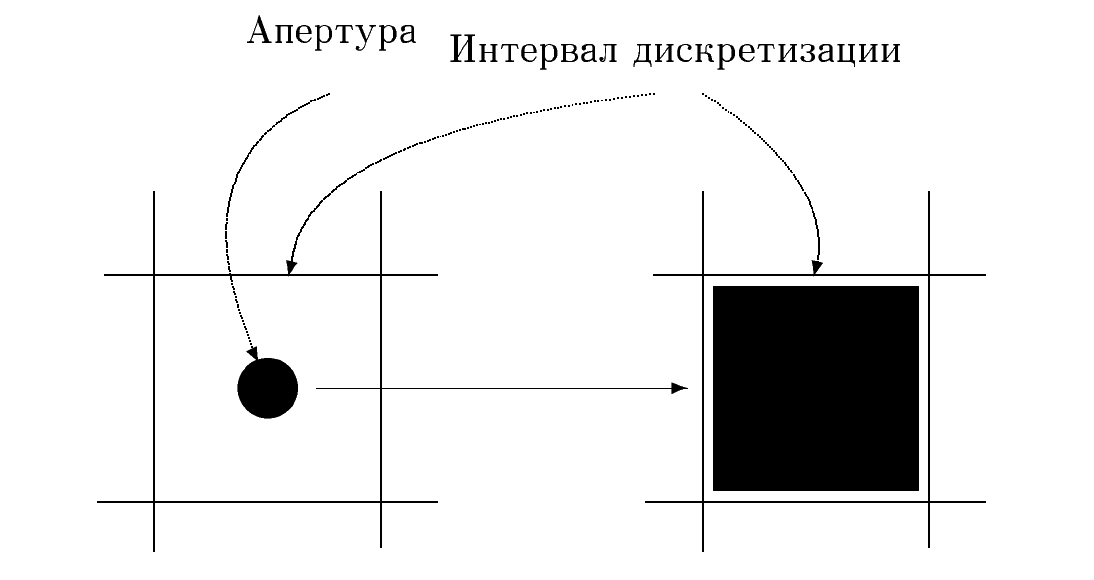
Рис. 6 На рис.6 показан пример сканирования фрагмента изображения при размере апертуры, меньшем чем интервал дискретизации или шаг сканирования.
|