-
-
Как продвинуть сайт на первые места?Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.Ускорение продвиженияЕсли вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги. Начать продвижение сайта
-
Сервис онлайн-записи на собственном Telegram-ботеТот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
| Неровнота при разной распрямленности волокон |
|
Страница 1 из 8
Введение Неровнота любого продукта - один из важнейших показателей продукта, возникающей на любом переходе. Цель работы - исследование неровноты, возникающей вследствие утонения продукта в Е раз. На схеме изображен процесс вытягивания ленты в вытяжном приборе, на выходе получают утоненную ленту. Cвх Известно, что абсолютная величина квадратичной неровноты ленты соответствует представленной ниже формуле (1), в этом случае неровнота на выходе будет значительно больше неровноты на входе,
Где
Далее в работе для упрощения принимаем неровноту на входе равной нулю. Тогда из формулы (1) получаем:
Где
Проведем анализ этой неровноты при разной распрямленности волокон. Работа, посвященная анализу этой неровноты, состоит из двух частей: 1 часть - все волокна ориентированы вдоль оси ленты и параллельны оси; 2 часть - все волокна находятся под углом к оси ленты.
Часть 1 1. Волокна распрямлены и ориентированы вдоль оси 1.1. Толщина ленты, дисперсия и коэффициент вариации
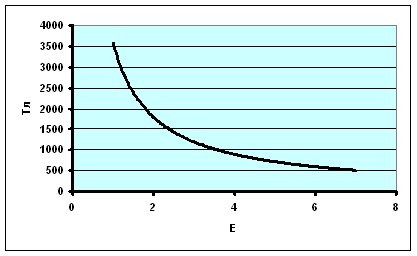
Где Т - линейная плотность волокна; N - число волокон в сечении; Е - общая вытяжка.
Рис.1.Зависимость толщины ленты от общей вытяжки
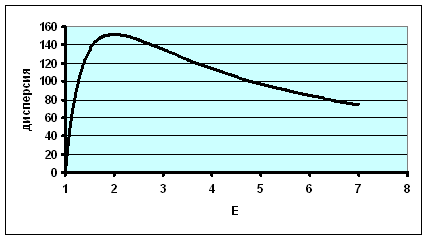
Эта зависимость является экстремальной, так как имеет точку экстремума. Для того. чтобы доказать это возьмем первую производную по дисперсии (ф-ла (4))и приравняем к нулю:
Рис.2.Зависимость дисперсии от общей вытяжки
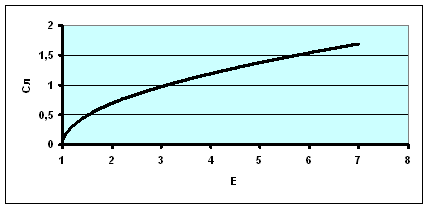
Рис.3.Зависимость коэффициента вариации от общей вытяжки
|
Свых
(1)
- неровнота на входе по числу волокон;
- неровнота на выходе по числу волокон;
- неровнота при утонении.
(2)
, (3)
, (4)
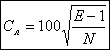, (5)
, 
