| Неровнота при разной распрямленности волокон |
|
Страница 4 из 8
4. Волокна имеют петлистость и ориентированы вдоль всей оси ленты
Петлистость 4.1. Коэффициент распрямленности рассчитывается по формуле (18)
Где 4.2. Коэффициент петлистости рассчитывается по формуле (19):
4.3. Дисперсия и коэффициент вариации
Где Т - линейная плотность волокна; N - число волокон в сечении; Е - общая вытяжка;
4.4. Строим графики зависимости дисперсии и коэффициента вариации от общей вытяжки (через коэффициент петлистости)
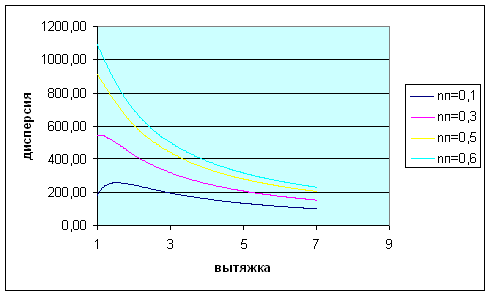
Рис.17. Зависимость дисперсии от общей вытяжки
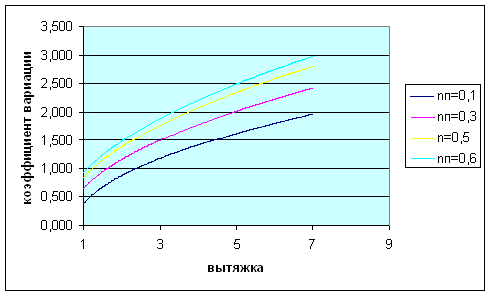
Рис.18. Зависимость коэффициента вариации от общей вытяжки Вывод: Чем больше вытяжка, тем больше коэффициент вариации; чем больше коэффициент петлистости, тем больше коэффициент вариации. 4.5. Так как нам известна зависимость коэффициента петлистости и коэффициента распрямленности из формулы (19), то подставим его в формулу (21) и получим новую формулу для коэффициента вариации (22)
Где N - число волокон в сечении; Е - общая вытяжка;
4.6. Строим график зависимости коэффициента вариации от общей вытяжки (через коэффициент распрямленности)
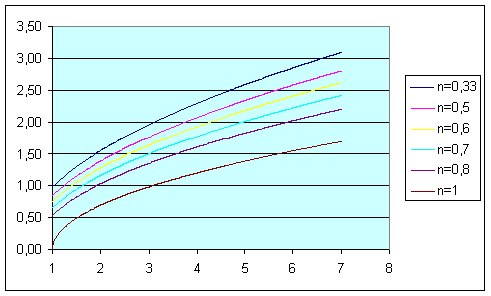
Рис.19. Зависимость коэффициента вариации от общей вытяжки Вывод: Чем больше вытяжка, тем больше коэффициент вариации; чем больше коэффициент распрямленности, тем меньше коэффициент вариации. 4.7. Построим графики зависимости дисперсии и коэффициента вариации от коэффициента петлистости. Таблица 4. Расчет дисперсии и коэффициента вариации (для коэффициента петлистости)
4.8. Строим графики зависимости дисперсии и коэффициента вариации от коэффициента петлистости
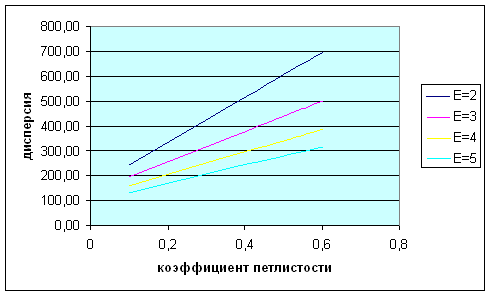
Рис.20. Зависимость дисперсии от коэффициента петлистости
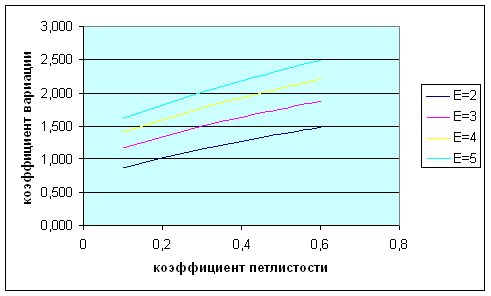
Рис.21. Зависимость коэффициента вариации от коэффициента петлистости Вывод: При увеличение коэффициента петлистости увеличивается коэффициент вариации и дисперсия. Общий вывод: Числовые значения коэффициентов вариации по формуле (21) и по формуле (22) равны, при условии, что Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
|
, (18)
- коэффициент петлистости
, 
,
, (20)
, (21)
, (22)
- коэффициент распрямленности.
. Для того, чтобы рассчитать коэффициент петлистости надо обязательно знать числовое значение коэффициента распрямленности и наоборот.