-
Как продвинуть сайт на первые места?Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.Ускорение продвиженияЕсли вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги. Начать продвижение сайта
-
-
Сервис онлайн-записи на собственном Telegram-ботеТот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
| Неровнота при разной распрямленности волокон |
|
Страница 2 из 8
2. Волокна изогнуты и ориентированы вдоль оси ленты
Изогнутость 2.1. Коэффициент распрямленности
Где 2.2. Коэффициент изогнутости определяется по формуле (8)
Где 2.3. Дисперсия и коэффициент вариации
Где Т - линейная плотность волокна; N - число волокон в сечении; Е - общая вытяжка;
2.4. Строим графики зависимости дисперсии и коэффициента вариации от общей вытяжки (через коэффициент изогнутости)
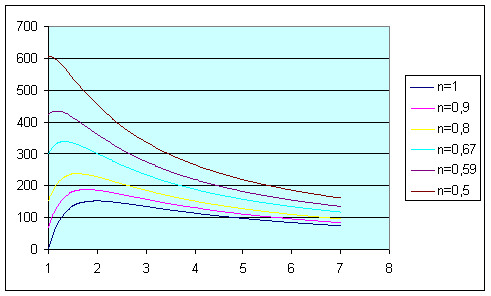
Рис.4. Зависимость дисперсии от общей вытяжки Эта зависимость является экстремальной, так как имеет точку экстремума. Для того. чтобы доказать это возьмем первую производную по дисперсии (ф-ла (9))и приравняем к нулю:
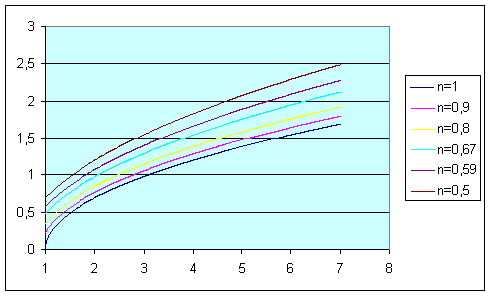
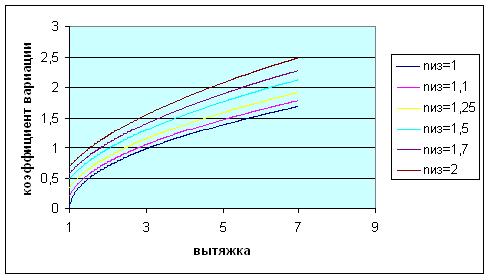
Рис.5. Зависимость коэффициента вариации от общей вытяжки Вывод: Чем больше вытяжка, тем больше коэффициент вариации; чем больше коэффициент изогнутости, тем больше коэффициент вариации. 2.5. Так как нам известен коэффициент распрямленности из формулы (7), то подставим его в формулу (9) и (10) и получим новые формулы для коэффициента вариации (12) и дисперсии (11)
Где Т - линейная плотность волокна; N - число волокон в сечении; Е - общая вытяжка;
2.6. Строим графики зависимости дисперсии и коэффициента вариации от общей вытяжки (через коэффициент распрямленности)
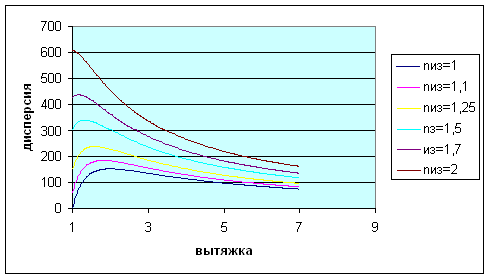
Рис.6. Зависимость дисперсии от общей вытяжки
Рис.7. Зависимость коэффициента вариации от общей вытяжки Вывод: Чем больше вытяжка, тем больше коэффициент вариации; чем больше коэффициент распрямленности, тем меньше коэффициент вариации. 2.7. Коэффициент распрямленности обратно пропорционален коэффициенту изогнутости, чтобы доказать это наглядно рассмотрим несколько графиков, а именно графики зависимости этих коэффициентов от дисперсии и коэффициента вариации. Таблица 1. Расчет дисперсии и коэффициента вариации (для коэффициента изогнутости)
2.8. Строим графики зависимости дисперсии и коэффициента вариации от коэффициента изогнутости
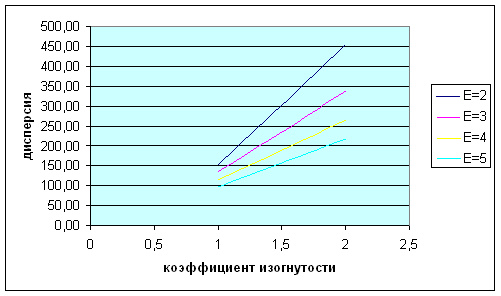
Рис.8. Зависимость дисперсии от коэффициента изогнутости
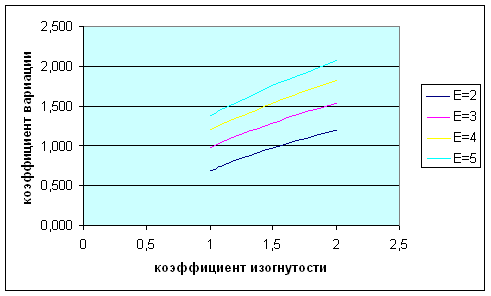
Рис.9. Зависимость коэффициента вариации от коэффициента изогнутости Вывод: При увеличение коэффициента изогнутости увеличевается коэффициент вариации и дисперсия. Таблица 2. Расчет дисперсии и коэффициента вариации (для коэффициента распрямленности)
2.9. Строим графики зависимости дисперсии и коэффициента вариации от коэффициента распрямленности
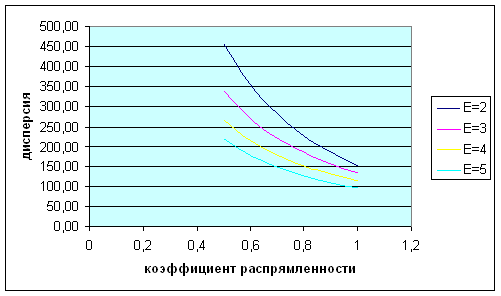
Рис.10. Зависимость дисперсии от коэффициента распрямленности
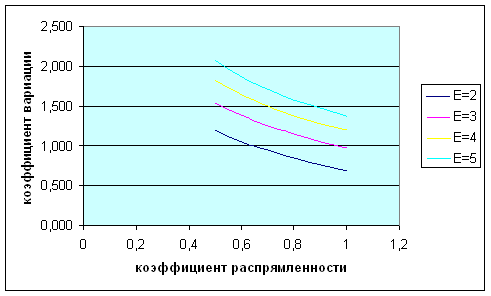
Рис.11. Зависимость коэффициента вариации от коэффициента распрямленности Вывод: При увеличение коэффициента распрямленности уменьшается коэффициент вариации и дисперсия. Общий вывод: Числовые значения коэффициентов вариации по формуле (10) и по формуле (12) равны, при условии, что коэффициент изогнутости будет обратно пропорционален коэффициенту распрямленности. Для того, чтобы рассчитать коэффициент изогнутости надо обязательно знать числовое значение коэффициента распрямленности и наоборот. |
, (6)
, (7)
- коэффициент изогнутости
, 
, 
, (8)
- угол наклона участка волокна горизонтальной к оси.
, (9)
, (10)
, (11)
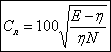, (12)
- коэффициент распрямленности.
