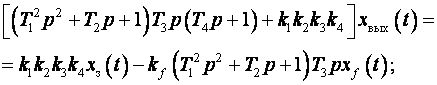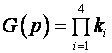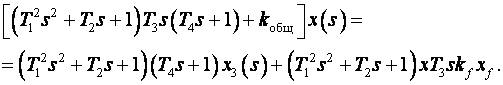| Исследование характеристик систем автоматического управления и их элементов с помощью ПЭВМ |
|
Страница 1 из 2 Исследование динамических характеристик элементов систем автоматического управления (САУ) Независимо от конкретного исполнения и функционального назначения элементы САУ при исследовании ее динамики представляются в виде динамических звеньев. Под динамическим звеном понимается математическая модель элемента, объекта или части системы. Если звено представляется дифференциальным уравнением не выше второго порядка, оно называется элементарным: T12 Из этого уравнения можно получить ряд более простых уравнений, которые характеризуют типовые элементарные динамические звенья: безынерционное, инерционные 1-го и 2-го порядка, колебательное, интегрирующее, дифференцирующее. Сложное динамическое звено представляет собой совокупность элементарных звеньев. Автоматическая система, включающая в себя бесчисленное множество элементов и объектов, может быть представлена конечным небольшим числом динамических звеньев. Динамическая характеристика связана с понятием переходного процесса и определяется передаточной функцией, частотной передаточной функцией и переходной функцией. Передаточной функцией называется отношение изображений по Лапласу выходного и входного воздействий с нулевыми начальными условиями:
Частотной передаточной функцией называется отношение изображений по Фурье выходного и входного воздействий с нулевыми начальными условиями:
Амплитудная частотная характеристика Фазовая частотная характеристика , Для анализа элементов САУ строится годограф частной передаточной функции (амплитудно-фазовая частотная характеристика) – геометрическое место точек концов вектора Переходная функция – это функциональная зависимость выходного воздействия от времени при подаче на вход ступенчатой единичной функции 1 с нулевыми начальными условиями. Типовые динамические звенья Безынерционное звено Безынерционным (усилительным) называется звено, характеризуемое и в статике, и в динамике алгебраическим уравнением:
Передаточная функция звена
Частотная передаточная функция
Рис. 1.1 Частотные характеристики и переходная функция безынерционного звена Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение Инерционное звено первого порядка
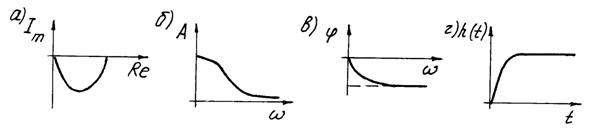
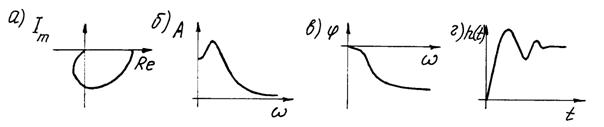
Передаточная функция и частотная передаточная функция (рис. 1.2, а)
Амплитудная и фазовая частотные характеристики (рис. 1.2, б, в)
Переходная функция (рис. 1.2, г)
Рис. 1.2 Частотные характеристики и переходная функция инерционного звена первого порядка Инерционное звено второго порядка
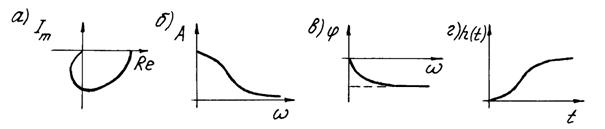
Передаточная функция и частотная передаточная функция (рис. 1.3, а)
Рис. 1.3 Частотные характеристики и переходная функция инерционного звена второго порядка Амплитудная и фазовая частотные характеристики (рис. 1.3, б, в)
Переходная функция, согласно корням характеристического уравнения T12p2 + T2p + 1 = 0
Колебательное звено
при условии: T22 – 4T12 < 0. Рис. 1.4 Частотные характеристики и переходная функция колебательного звена Интегрирующее звено
Передаточная функция и частотная передаточная функция Амплитудная и фазовая частотные характеристики Переходная функция h(t) =
Рис. 1.5 Частотные характеристики и переходная функция интегрирующего звена Дифференцирующее звено
Характеристики звена:
Рис. 1.6 Частотные характеристики и переходная функция дифференцирующего звена Исследование динамических характеристик типовых звеньев САР можно провести аналитически с учетом фактических значений параметров K и i или с использованием специальных программ (см. комплекс “Avtomat”). Для исследования динамических характеристик элементов и объектов САУ необходимо получить численные значения параметров динамических звеньев – коэффициента передачи К (статический параметр) и постоянной времени Т (динамический параметр). Коэффициент передачи можно получить из графика статической характеристики элемента, найденной либо аналитически на основании использования физического закона, описывающего реальный процесс, протекающий в элементе, либо экспериментально. Постоянную времени можно определить расчетным путем или путем выбора приведенных в справочных таблицах значений (как правило, принимаются средние значения). Исследование динамических характеристик САУ Передаточные функции автоматических систем При анализе автоматической системы рассматриваются передаточные функции, относящиеся к самой системе. Передаточная функция разомкнутой системы Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Передаточная функция замкнутой системы определяется по соответствующему входу. По заданному воздействию
по возмущению Частотная передаточная функция САУ Частотная передаточная функция САУ получается из передаточной функции системы заменой S на iw:
Переходный процесс САУ Переходный процесс может быть вызван двумя причинами: начальным отклонением координат состояния системы и появлением внешнего входного воздействия. Это собственные движения в системе. Для построения переходного процесса необходимо получить математическую модель САУ. Исходные дифференциальные уравнения системы составляются двумя методами: общим и с помощью передаточных функций. Первый метод основан на имеющихся дифференциальных уравнениях элементов системы, записанных в операционной форме. Составляется система уравнений, которая разрешается относительно Xвых:
где Систему уравнений можно разрешить относительно ошибки, тогда
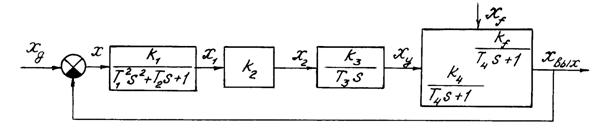
Допустим, САУ представлена структурной схемой (рис. 2.1).
Рис. 2.1 Структурная схема САУ Система дифференциальных уравнений:
Использовав метод подстановки, разрешим систему уравнений относительно Xвых:
D(p) = a0 p4 + a1 p3 + a2 p2 +a3 p + a4;
N(p) = c0 p3 + c1 p2 + c2 p. Аналогично можно разрешить систему уравнений относительно ошибки x. Второй метод основан на передаточных функциях системы. Необходимо получить передаточную функцию разомкнутой системы
где k1, k2, k3, k4 = kобщ k1 k2 k3 k4 = kобщ. Передаточная функция управляемого объекта по возмущению
Подставив эти выражения в уравнение, разрешенное относительно ошибки, получим:
Аналогично составляем уравнения относительно Xвых:
Динамические характеристики САР можно получить аналитически с учетом фактических значений параметров всех звеньев или с использованием специальных программ (см. комплекс “Avtomat”). Устойчивость САУ Устойчивость системы – это ее свойство возвращаться в состояние установившегося равновесия после снятия возмущения, нарушившего это равновесие. Устойчивость – необходимое условие для автоматической системы: Прямой способ исследования устойчивости системы заключается в нахождении решения однородного дифференциального уравнения. Переходные процессы носят затухающий характер. Для упрощения анализа устойчивости находят корни характеристического полинома D(s)=0 . Система является устойчивой, если все вещественные корни и действительные части комплексных корней отрицательны. Аналитическое нахождение корней полинома возможно до третьего порядка (включительно), а при порядке более третьего используют средства вычислительной техники (см. комплекс “Avtomat”). Широко распространен метод Найквиста для проверки устойчивости САР. Система устойчива, если годограф частотной характеристики разомкнутой системы не охватывает точку с координатами (-1,0i) . Этот метод реализован в программном комплексе “Avtomat”.
|



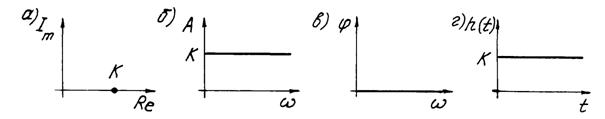
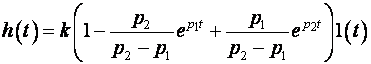 .
.
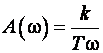 ;
; 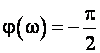 .
.