| Оценка точности стандартного метода определения линейных размеров |
|
Страница 3 из 10
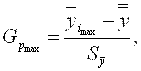
Методика обработки полученных данных Определение прецизионности стандартизированного метода измерений Анализ экспериментальных данных в целях обнаружения резко выделяющихся результатов Для идентификации резко выделяющихся результатов (выбросов) используются два типа статистических критериев – критерий Граббса и критерий Кохрена. Критерий Граббса применяется для проверки наличия выбросов в величинах средних арифметических значений результатов испытаний в лабораториях в пределах одного уровня. Расчетное значение критерия Граббса находится по формулам
и
где общее среднее арифметическое значение результата испытания, вычисляемое по формуле
где и соответственно максимальные и минимальные значения средних арифметических результатов испытаний, полученных в лабораториях;
Определив по формулам (2) или (3) расчетное значение критерия Граббса, его величину сравнивают с табличным значением при доверительной вероятности Рд = 0,95. Если расчетное значения критерия Граббса меньше (или равно) табличного, то проверяемую величину не считают выбросом и оставляют для дальнейшей статистической обработки. При выполнении неравенства проверяемое значение считают выбросом и исключают из дальнейших расчетов. Критерий Кохрена используется для оценки однородности (отсутствия выбросов) дисперсий результатов испытаний, полученных в лабораториях на исследуемом уровне измеряемой характеристики. Расчетное значение критерия Кохрена находится по формуле
где
где ? число результатов измерений в i-ой лаборатории на данном уровне;
После вычисления по формуле (6) расчетного значения критерия Кохрена его величину сравнивают с табличным значением при доверительной вероятности Рд = 0,95. Если расчетное значения критерия Кохрена меньше (или равно) табличного, то проверяемую величину не считают выбросом и оставляют для дальнейшей статистической обработки. В противном случае, если то проверяемое значение считают выбросом и исключают из дальнейших расчетов. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
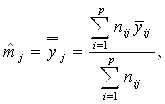
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение Расчет оценок прецизионности и средних значений Расчет оценок прецизионности и средних значений производится для каждого из пяти уровней раздельно. Вычисление начинается с определения средних значений в базовых элементах (9) где число измерений в i-ой лаборатории на уровне j , (т. е. в ij-м базовом элементе); yijk k-й из этих результатов измерений Значения рекомендуется рассчитывать с точностью на одну значащую цифру большей, чем исходные данные. Величину рассеяния (разброса) в базовых элементах находят как
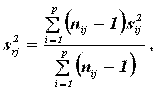
Общее среднее значение
где р – число лабораторий, принимающих участие в эксперименте. Дисперсия повторяемости находится по формуле
а межлабораторная дисперсия как
где (14) а среднее арифметическое значение числа измерений по всем базовым элементам (лабораториям)
Тогда дисперсия воспроизводимости может быть найдена как
Так как при расчетах используется достаточно ограниченная выборка, то вычисленная величина может принять отрицательное значение и тогда ее приравнивают к нулю. Наличие характеристик прецизионности без сравнения с соответствующими нормативами не дает исчерпывающего ответа о точности осуществляемых измерений. Для ответа на данный вопрос результаты расчетов необходимо сравнить с нормативами повторяемости и воспроизводимости, соответственно пределом повторяемости и пределом воспроизводимости. Рассмотрим, как определяются значения пределов повторяемости и воспроизводимости. Например, если в одной лаборатории в условиях повторяемости выполнены две группы измерений со средними арифметическими значениями соответственно и и числом испытаний в группах и , то предел повторяемости r, равный критической разности при доверительной вероятности составит
В большинстве случаев в вариантах заданий на выполнение курсовой работы = = 2, т. е. предполагается, что четыре повторных результата измерения показателя качества получены путем проведения двух групп измерений по два опыта в каждой. Если в двух лабораториях условиях повторяемости выполнено по одной серии измерений со средними арифметическими значениями соответственно и с числом испытаний в сериях и , то предел воспроизводимости R, равный критической разности при доверительной вероятности , составит Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
при этом = = 4, так как согласно заданию в каждой из лабораторий выполнялись по 4 повторных опыта. Статистический анализ данных эксперимента по оценке прецизионности дополняется установлением функциональной зависимости между значениями прецизионности и средними значениями m уровней. Если на графике зависимости от аргумента хорошо видна определенная зависимость, например, прямо пропорциональная, то можно ограничиться графической аппроксимацией. В иных случаях рекомендуется проводить более сложную аналитическую аппроксимацию. После аппроксимации зависимости, окончательными значениями и считают сглаженные значения, полученные для этой зависимости для заданных величин m. Если оценивают, как независящее от то для окончательной оценки значения среднего квадратического отклонения повторяемости используют выражение
|



 (2)
(2)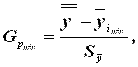 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (8)
(8)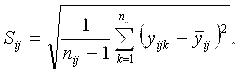 (10)
(10) (11)
(11) (12)
(12) (13)
(13) (15)
(15) (17)
(17)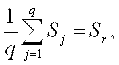 (19)
(19)