| Оценка точности стандартного метода определения линейных размеров |
|
Страница 8 из 10
Оценка зависимости прецизионности от общего среднего для каждого уровня В данной курсовой работе в результате расчетов получены данные, приведенные в таблице Таблица 3.3.1 – Результаты расчетов
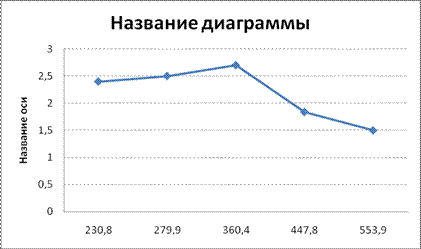
Нанесем координаты точек на график и проведем аппроксимацию функциональной зависимости. Зависимость прецизионности Srj и SRj от общего среднего для каждого уровня испытаний отражена на рисунке . Рисунок 3.3.1 – График функций Srj и SRj по аргументу
Как можно видеть из графика, между прецизионностью и общим средним для каждого уровня не существует функциональная зависимость. А в случае, если оценивают, как независящее от , то для окончательной оценки значения среднего квадратического отклонения повторяемости используют формулу (19)
Вычисление систематической погрешности стандартного метода измерений Исходные данные и результаты расчетов систематической погрешности метода испытаний приведены в таблицах: по каждому уровню отдельно. Расчеты проводились по формулам (24-27). Таблица 3.4.1 – Исходные данные и результаты расчета систематической погрешности метода испытаний для первого уровня
Так как доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, систематическая погрешность метода измерения при уровне значимости незначима. Таблица 3.4.2 – Исходные данные и результаты расчета систематической погрешности метода испытаний для второго уровня
Так как доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, систематическая погрешность метода измерения при уровне значимости незначима. Таблица 3.4.3 – Исходные данные и результаты расчета систематической погрешности метода испытаний для третьего уровня
Так как доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, систематическая погрешность метода измерения при уровне значимости незначима. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение Таблица 3.4.4 – Исходные данные и результаты расчета систематической погрешности метода испытаний для четвертого уровня
Так как доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, систематическая погрешность метода измерения при уровне значимости незначима. Таблица 3.4.5 – Исходные данные и результаты расчета систематической погрешности метода испытаний для пятого уровня
Так как доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, систематическая погрешность метода измерения при уровне значимости незначима.
|