| Оценка точности стандартного метода определения линейных размеров |
|
Страница 4 из 10
Определение правильности стандартного метода измерений Вычисление систематической погрешности стандартного метода измерений При этом методе общее среднее значение m заменяется на
где μ – принятое опорное значение измеряемой характеристики; – систематическая погрешность метода измерений. Тогда модель принимает следующий вид:
где B - это лабораторная составляющая систематической погрешности стандартного метода измерений, т. е. часть результата измерения, представляющая межлабораторную вариацию. Поэтому систематическую погрешность лаборатории выражают ка
Тогда модель (20) может быть представлена в виде
Основной целью эксперимента является оценка значения систематической погрешности метода измерений и установление ее статистической значимости. Оценку систематической погрешности стандартного метода, полученную, например, при оценке компетентности лабораторий, выражают уравнением
где может быть положительным или отрицательным;
Доверительный интервал при доверительной вероятности для систематической погрешности метода измерения рассчитывается по формуле
где
и
Если доверительный интервал, рассчитанный по формуле (25), включает в себя нулевое значение, то систематическая погрешность метода измерения при уровне значимости незначима, в противном случае ее считают значимой. Вычисление систематической погрешности лаборатории Оценка систематической погрешности лаборатории при реализации конкретного стандартного метода измерений основывается на проведении эксперимента в этой одной лаборатории при условии, что ранее в результате межлабораторного эксперимента по оценке прецизионности найдено среднеквадратическое отклонение повторяемости метода . Оценку систематической погрешности лаборатории
где - среднее значение результатов измерений, вычисляют как
Доверительный интервал при доверительной вероятности для систематической погрешности лаборатории определяется неравенством
где
Если доверительные интервалы, рассчитанные по формулам (25) и (30) включают в себя нулевые значения, то систематическая погрешность метода измерения и систематическая погрешность лаборатории при уровне значимости незначимы, в противном случае их считают значимыми. Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение В результате проведения совместного оценочного эксперимента по применению стандартного метода испытаний (на идентичном материале) по ГОСТ 6611.1–73 «Нити текстильные. Метод определения линейной плотности» получены экспериментальные данные, представленные в приложении А.
|



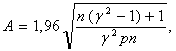 (26)
(26)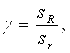 (27)
(27) (29)
(29)