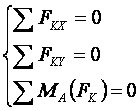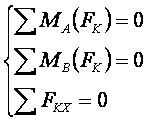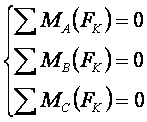|
Страница 5 из 8
ЗАДАЧА 2. РАВНОВЕСИЕ ПЛОСКОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩЕЙ НА РАМУ
Рассчитать величины реакций связей изображенной на рисунке рамы с использованием приведенных на схемах и таблице 2 исходных данных.
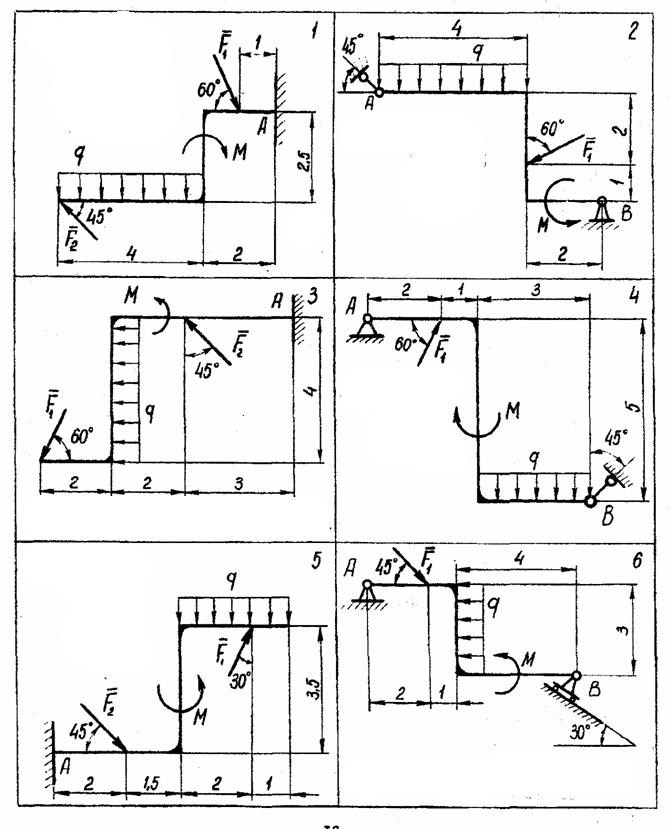
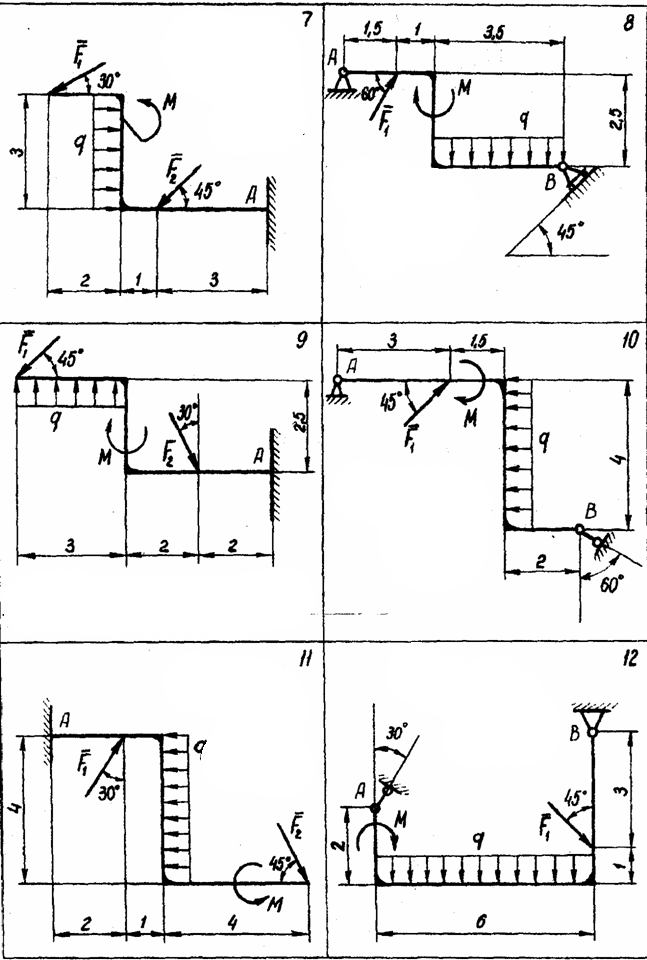
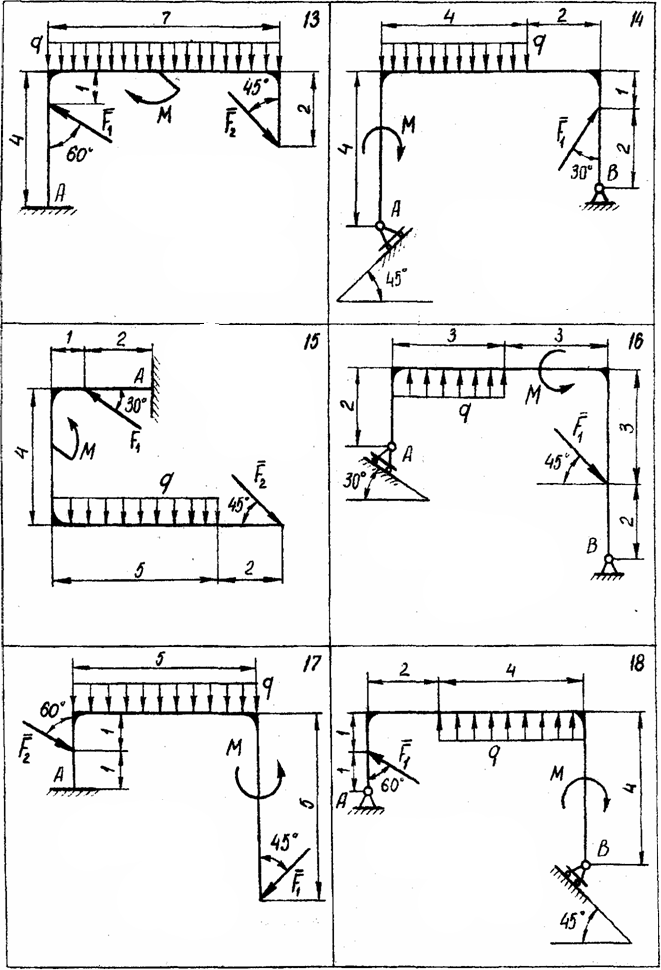
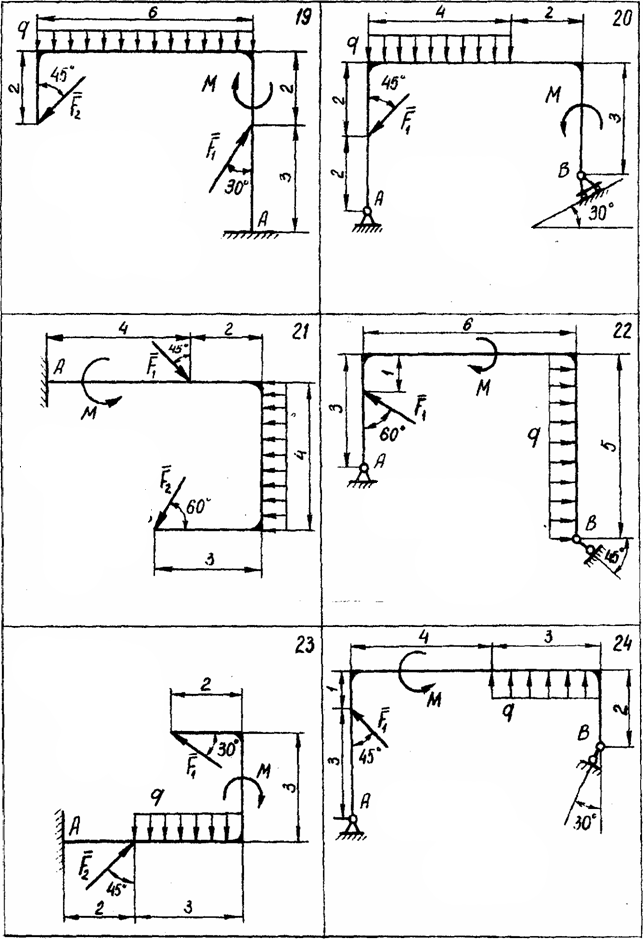
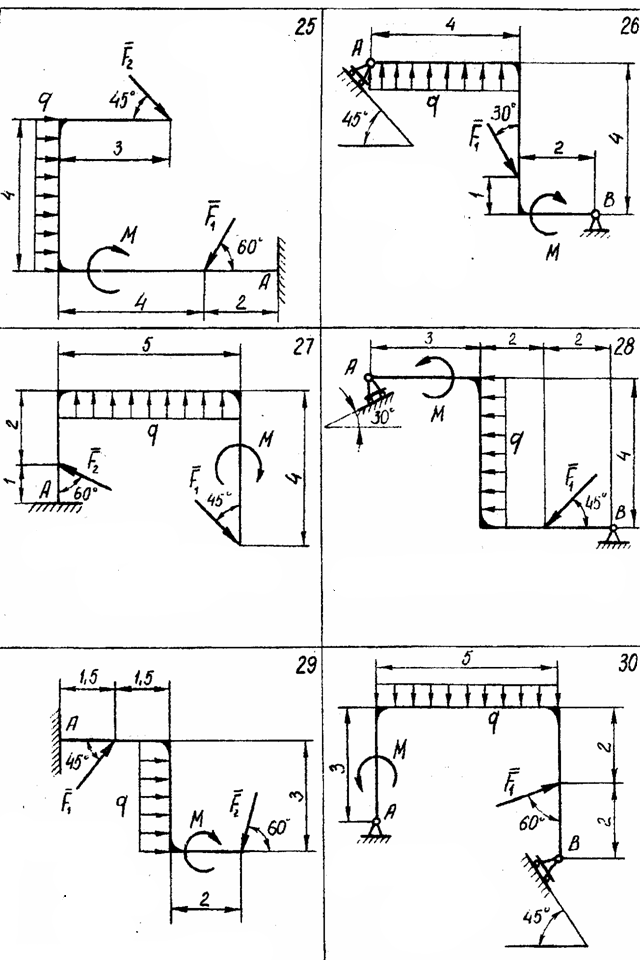
Таблица 2. Исходные данные к задаче 2.
|
№ варианта
|
№ схемы
|
F1, Н
|
F2, Н
|
q, Н/м
|
М, Н/м
|
|
1
|
1
|
10
|
5
|
2
|
20
|
|
2
|
2
|
10
|
-
|
1
|
50
|
|
3
|
3
|
10
|
20
|
3
|
40
|
|
4
|
4
|
20
|
-
|
4
|
70
|
|
5
|
5
|
10
|
20
|
2
|
15
|
|
6
|
6
|
15
|
-
|
4
|
50
|
|
7
|
7
|
5
|
10
|
3
|
15
|
|
8
|
8
|
20
|
-
|
4
|
30
|
|
9
|
9
|
20
|
10
|
3
|
20
|
|
10
|
10
|
10
|
-
|
2.5
|
20
|
|
11
|
11
|
30
|
5
|
2
|
25
|
|
12
|
12
|
15
|
-
|
2
|
90
|
|
13
|
13
|
15
|
30
|
2
|
40
|
|
14
|
14
|
20
|
-
|
3
|
45
|
|
15
|
15
|
30
|
20
|
4
|
50
|
|
16
|
16
|
20
|
-
|
5
|
50
|
|
17
|
17
|
5
|
10
|
1
|
70
|
|
18
|
18
|
40
|
-
|
2
|
120
|
|
19
|
19
|
10
|
20
|
1
|
25
|
|
20
|
20
|
25
|
-
|
3
|
30
|
|
21
|
21
|
15
|
20
|
2
|
120
|
|
22
|
22
|
15
|
-
|
2
|
25
|
|
23
|
23
|
25
|
40
|
5
|
50
|
|
24
|
24
|
10
|
-
|
2
|
20
|
|
25
|
25
|
30
|
20
|
2.5
|
40
|
|
26
|
26
|
50
|
-
|
2.5
|
60
|
|
27
|
27
|
25
|
15
|
6
|
50
|
|
28
|
28
|
25
|
-
|
2.5
|
60
|
|
29
|
29
|
10
|
50
|
10
|
150
|
|
30
|
30
|
25
|
-
|
5
|
40
|
|
31
|
1
|
15
|
20
|
4
|
60
|
|
32
|
2
|
20
|
-
|
3
|
80
|
|
33
|
3
|
20
|
10
|
4
|
60
|
|
34
|
4
|
15
|
-
|
2
|
90
|
|
35
|
5
|
20
|
15
|
4
|
45
|
|
36
|
6
|
25
|
-
|
2
|
70
|
|
37
|
7
|
15
|
5
|
4
|
45
|
|
38
|
8
|
30
|
-
|
2
|
50
|
|
39
|
9
|
10
|
15
|
4
|
40
|
|
40
|
10
|
25
|
-
|
4
|
30
|
|
41
|
11
|
15
|
20
|
3
|
50
|
|
42
|
12
|
20
|
-
|
4
|
50
|
|
43
|
13
|
20
|
10
|
3
|
60
|
|
44
|
14
|
10
|
-
|
2
|
70
|
|
45
|
15
|
15
|
30
|
2
|
90
|
|
46
|
16
|
15
|
-
|
3
|
30
|
|
47
|
17
|
15
|
20
|
2
|
50
|
|
48
|
18
|
25
|
-
|
4
|
70
|
|
49
|
19
|
20
|
10
|
2
|
50
|
|
50
|
20
|
15
|
-
|
4
|
70
|
|
51
|
21
|
25
|
15
|
3
|
100
|
|
52
|
22
|
25
|
-
|
4
|
50
|
|
53
|
23
|
15
|
30
|
4
|
70
|
|
54
|
24
|
25
|
-
|
3
|
50
|
|
55
|
25
|
20
|
30
|
3
|
60
|
|
56
|
26
|
40
|
-
|
4
|
20
|
|
57
|
27
|
30
|
10
|
4
|
70
|
|
58
|
28
|
15
|
-
|
4
|
90
|
|
59
|
29
|
25
|
20
|
6
|
120
|
|
60
|
30
|
30
|
-
|
3
|
110
|
|
61
|
1
|
24
|
15
|
6
|
14
|
|
62
|
2
|
22
|
-
|
5
|
35
|
|
63
|
3
|
18
|
12
|
5
|
55
|
|
64
|
4
|
14
|
-
|
8
|
50
|
|
65
|
5
|
32
|
30
|
7
|
60
|
|
66
|
6
|
14
|
-
|
8
|
24
|
|
67
|
7
|
24
|
25
|
9
|
25
|
|
68
|
8
|
50
|
-
|
5
|
80
|
|
69
|
9
|
28
|
20
|
7
|
15
|
|
70
|
10
|
35
|
-
|
6,5
|
45
|
|
71
|
11
|
45
|
10
|
5
|
35
|
|
72
|
12
|
32
|
-
|
8
|
26
|
|
73
|
13
|
36
|
6
|
9
|
18
|
|
74
|
14
|
28
|
-
|
7
|
29
|
|
75
|
15
|
21
|
9
|
7
|
34
|
|
76
|
16
|
40
|
-
|
8
|
90
|
|
77
|
17
|
22
|
35
|
2,5
|
82
|
|
78
|
18
|
12
|
-
|
12
|
26
|
|
79
|
19
|
32
|
30
|
7
|
16
|
|
80
|
20
|
35
|
-
|
8
|
55
|
|
81
|
21
|
40
|
32
|
9
|
65
|
|
82
|
22
|
60
|
-
|
11
|
84
|
|
83
|
23
|
75
|
25
|
12
|
36
|
|
84
|
24
|
56
|
-
|
8
|
95
|
|
85
|
25
|
44
|
68
|
8
|
78
|
|
86
|
26
|
82
|
-
|
8
|
140
|
|
87
|
27
|
55
|
80
|
8
|
95
|
|
88
|
28
|
44
|
-
|
8
|
115
|
|
89
|
29
|
64
|
36
|
12
|
68
|
|
90
|
30
|
72
|
-
|
9
|
84
|
|
91
|
1
|
46
|
68
|
9
|
105
|
|
92
|
2
|
34
|
-
|
12
|
88
|
|
93
|
3
|
35
|
67
|
9
|
110
|
|
94
|
4
|
42
|
-
|
12
|
64
|
|
95
|
5
|
66
|
24
|
12
|
94
|
|
96
|
6
|
48
|
-
|
12
|
66
|
|
97
|
7
|
33
|
72
|
12
|
88
|
|
98
|
8
|
74
|
-
|
9
|
56
|
|
99
|
9
|
62
|
44
|
12
|
99
|
|
100
|
10
|
55
|
-
|
12
|
84
|
Методические указания к решению задачи 2
Решение задач на равновесие твердого тела, независимо от взаимного расположения приложенных к телу сил, рекомендуется проводить в следующем порядке:
- выделить твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин;
- изобразить активные силы;
- если твердое тело несвободно, то, применив закон освобождаемости от связей, приложить к нему соответствующие реакции связей;
- рассмотреть равновесие данного несвободного твердого тела, как тела свободного, находящегося под действием активных сил и реакций связи;
- убедиться в том, что данная задача является статически определимой, т.е. число неизвестных величин не более трех;
- выбрать направление осей декартовых координат и точку (или точки) относительно которой предполагается составить уравнение моментов. Оси координат целесообразно направить так, чтобы некоторые неизвестные силы оказались перпендикулярными к этим осям. Тогда величины этих неизвестных сил в соответствующее уравнение проекций не войдут.
Точку, относительно которой должно быть составлено уравнение моментов, следует выбрать в точке пересечения линий действия двух неизвестных сил. Это дает возможность непосредственно определить из соответствующего уравнения моментов величину третьей неизвестной силы. Однако, если эта точка расположена так, что вычисление плеч при определении моментов сил представляет значительные трудности, то лучше уравнение моментов составить относительно другой точки, в которое войдут величины двух неизвестных сил, и затем совместно решить полученную систему уравнений;
7. составить уравнение равновесия твердого тела. При решении задачи используется любое из трех видов уравнений равновесия:
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
|
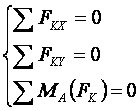
|
Если произвольная плоская система сил уравновешена, то алгебраическая сумма проекций всех сил на оси X и Y равна нулю, а также равна нулю алгебраическая сумма моментов всех сил относительно любой точки, лежащей на плоскости.
|
|
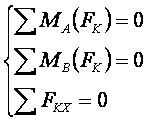
|
Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно двух любых точек, а также алгебраическая сумма проекций сил на ось, не перпендикулярную прямой проходящей через эти точки, равны нулю.
|
|
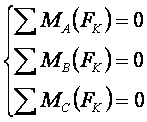
|
Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно любых трех точек, не лежащих на одной прямой, равны нулю.
|
- решить систему полученных уравнений равновесия и определить неизвестные величины. Если в результате решения знак величины какой-либо силы или момента окажется отрицательным, то это означает, что направление силы или момента противоположно тому, которое было предварительно выбрано;
- сделать проверку и убедиться, что неизвестные величины найдены верно.
|