| Теоретическая механика КР-1 |
|
Страница 6 из 8
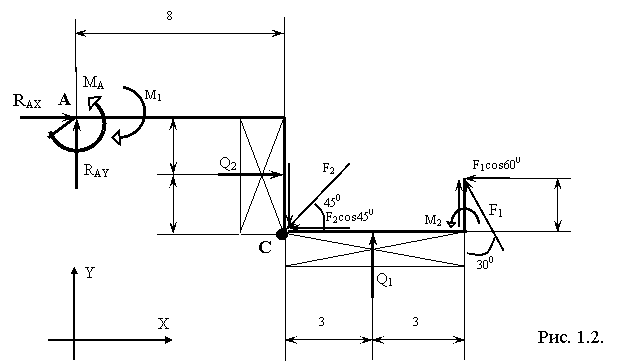
Примеры решения задачи 2 Задача 2.1. Консольная балка (рама). Балка (рама) с жесткой заделкой или жестким защемлением называется консолью. Жесткая заделка лишает балку (раму) всех трех степеней свободы: линейных перемещений вдоль осей Х и У и возможности поворота в плоскости этих осей. Соответственно в защемлении появляются три неизвестные величины: реакции RX, RY и реактивный момент заделки MA. Для их определения наиболее удобными являются уравнения: S FKX= 0 – для определения горизонтальной реакции RX S FKY= 0 – для определения вертикальной реакции RY S MA(FK) = 0 – уравнение моментов сил относительно точки заделки для определения реактивного момента MA, т.к. реакции RX и RY, приложенные в точке А, в уравнение не войдут (их моменты относительно точки А равны нулю). Рассмотрим решение задачи 1 на следующем примере: Рассчитать величины реакций связей изображенной на рисунке 1.1. рамы. Дано: F1=20 H; F2=30 H; M1= 60 H>*м; М2= 30 Н*м; q1 = 4 Н/м; q2 = 6 Н/м
Решение: 1. освобождаемся от связей и заменяем их реакциями. В данном случае связью для нашей рамы является жесткая заделка; 2. заменяем равномерно-распределенную нагрузку интенсивностью q сосредоточенной силой Q = q*L, где L- длина участка приложения нагрузки. Линия действия силы QQ проходит через середину участка L, занятого равномерно-распределенной нагрузкой. Q1= q1* L1 = 6*4 = 24H Q2= q2* L2 = 4*6 = 24Н
3. Задача статически определима, т. к. число неизвестных три: RAX; RAY; MA; 4. Выбираем направление осей декартовых координат; 5. Раскладываем все силы, лежащие под углом к балке, на две составляющие: По оси ОХ : F1 cos 60° и F2 cos 45° По оси OY : F1 cos 30° и F2 cos 45° (см. рис. 1.2.) 6. Для нахождения неизвестных воспользуемся системой уравнений равновесия: S FKX = 0 SFKY = 0 S MA(FK) = 0 7. Составим эти уравнения: S FKX = 0; RAX + Q2 – F2 cos450 – F1 cos600 = 0 (1) S FKY = 0; RAY – F2 cos450 + Q1 + F1 cos300 = 0 (2) S MA(FK) = 0; MA – M1 + Q2*2 – F2 cos450* 8 – F2 cos450* 4 + Q1*11 + M2 + F1 cos300*14 – F1 cos600*2 = 0 (3) 8. из (1) уравнения найдем величину реакции RAX RAX = – Q2 + F2 cos450 + F1 cos600 ; RAX = – 24 + 30 cos450 + 20 cos600 = 7,2 H ; Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
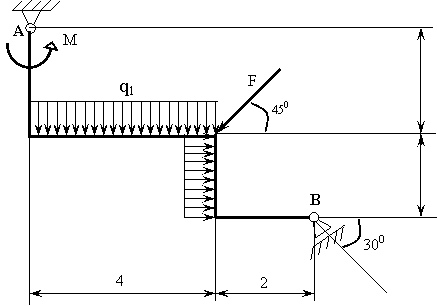
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок. — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта. — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы). — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание. SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение 9. из (2) уравнения определим величину реакции RAY RAY = F2 cos450 – Q1 – F1 cos300 ; RAY = 30 >cos450 – 24 – 20 cos300 = – 20,1 H ; Знак минус показывает, что направление реакции RAY противоположно выбранному; 10. из (3) уравнения рассчитаем величину реактивного момента МA MA = M1 – Q2*2 + F2 cos450* 8 + F2 cos450* 4 – Q1*11 – M2 – F1 cos300*14 + F1 cos600*2 ; MA = 60 - 24*2 + 30*8 cos450 + 30* 4 cos450 – 24*11 – 30 – 20*14 cos300 + 20*2 cos600 = – 249,9 H* м> ; Знак минус показывает, что направление реактивного момента MA противоположно выбранному; 11. сделаем проверку, для этого составим уравнение моментов всех сил, относительно точки С. S МС (FK МС (FK) = – RAY*8 – RAX* 4 + MA – M1 – Q2*2 + Q1*3 + M2 + F1 cos300*6 + F1 cos600*2 = 0; 20,1*8 – 7,2* 4 – 249,9 – 60 – 24*2 + 24* 3 + 30 + 20* 6 cos300 + 20* 2>cos600 = 0; 0 = 0 , следовательно величины реакций связей рассчитаны верно. Ответ: RAX = 7,2 H; RAY = – 20,1 H; MA = – 249,9 H*м Задача 2.2. Балка (рама) на двух опорах. Рассчитать величины реакций связей изображенной на рисунке 1.3. рамы. Дано: F=20H; F=20H; F=20H; q1=6H/м; q2=4H/м; M=50 H м
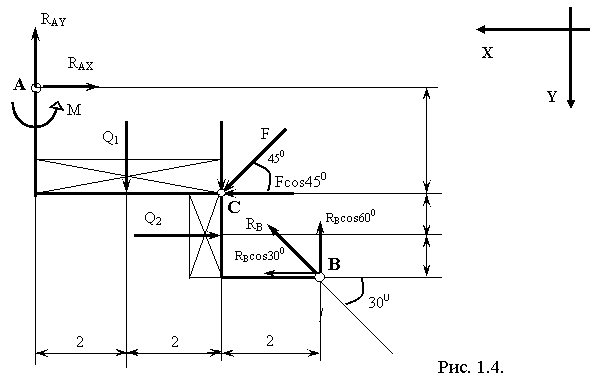
Решение: 1. освобождаемся от связей и заменяем их реакциями. В данном случае связями для нашей рамы являются шарнир А и шарнирно-подвижная опора В. В точке А рама может свободно поворачиваться около шарнира, но невозможны поступательные перемещения вдоль обеих координатных осей, направление этой реакции заранее неизвестно, поэтому заменим искомую силу двумя составляющими RXи RY, перпендикулярными друг другу. Шарнирно-подвижная опора В препятствует лишь поступательному перемещению рамы по нормали к опорной поверхности, поэтому реакция R такой опоры направлена по пересекающей ось шарнира прямой, перпендикулярной его опорной поверхности; 2. заменяем равномерно-распределенную нагрузку интенсивностью q сосредоточенной силой Q = q*L , где L-длина участка приложения нагрузки. Линия действия силы Q проходит через середину участка L, занятого равномерно-распределенной нагрузкой. Q1= q1* L1 = 6* 4 = 24H Q2= q2* L2 = 4* 2 = 8Н
3. задача статически определима, т. к. число неизвестных три: RAX ; RAY; RB; 4. выбираем направление осей декартовых координат; 5. раскладываем все силы лежащие под углом к балке на две составляющие: по оси OX: F cos 450 и RB cos 300 ; по оси OY: F cos 450 и RB cos 600 (см. рис. 1.4.); 6. для нахождения неизвестных воспользуемся системой уравнений равновесия: Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:— Разгрузит мастера, специалиста или компанию; — Позволит гибко управлять расписанием и загрузкой; — Разошлет оповещения о новых услугах или акциях; — Позволит принять оплату на карту/кошелек/счет; — Позволит записываться на групповые и персональные посещения; — Поможет получить от клиента отзывы о визите к вам; — Включает в себя сервис чаевых. Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе S FKX = 0 S FKY = 0 S MA(FK) = 0 7. составим эти уравнения: S FKX = 0; – RAX – Q2 + Fcos450 + RBcos300 = 0 (1) S FKY = 0; – RAY + Q1 + Fcos450 – RBcos600 = 0 (2) S MA(FK) = 0; M – Q1*<2 – Fcos450*4 – Fcos450*<3 + Q2*4 + RBcos600*<6 – RBcos300*<5=0 (3) 8. из (3) уравнения найдем величину реакции RB RBcos600*<6 – RBcos300*<5 = – M + Q1*2 + Fcos450*<4 + Fcos450*3 – Q2*<4 RB(cos600*6 – cos300*<5) = – M + Q1*<2 + Fcos450*4 + Fcos450*<3 – Q2*4
Знак минус показывает, что направление реакции RB противоположно выбранному; 9. из (1) уравнения определим величину реакции RAX RAX= – Q2 + Fcos450 + RBcos300 RAX= – 8 + 20cos450 – 48,9cos300 = – 36,2H Знак минус показывает, что направление реакции RAX противоположно выбранному; 10. из (2) уравнения рассчитаем величину реакции RAY RAY = Q1 + Fcos450 – RBcos600 RAY= 24 + 20cos450 + 48,9cos600 = 62,6H ; 11. сделаем проверку, для этого составим уравнение моментов всех сил относительно точки C. SMC(FK) = 0. В такое уравнение войдут все три искомые величины, т.к. линии действия ни одной из этих сил не проходят через точку С. SMC(FK)< = – RAY*4 – RAX*<3 + M + Q1*2 + Q2*<1 – RBcos300*<2 + RBcos600*<2 = 0; – 62,6*4 + 36,2*3 + 50 + 24*2 + 8*1 + 48,9 cos300*2 – 48,9cos600*2 = 0; 0 = 0, следовательно величины реакций связей рассчитаны верно. Ответ : RAX = – 36,2H RAY = 62,6H RB = – 48,9H
|