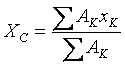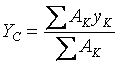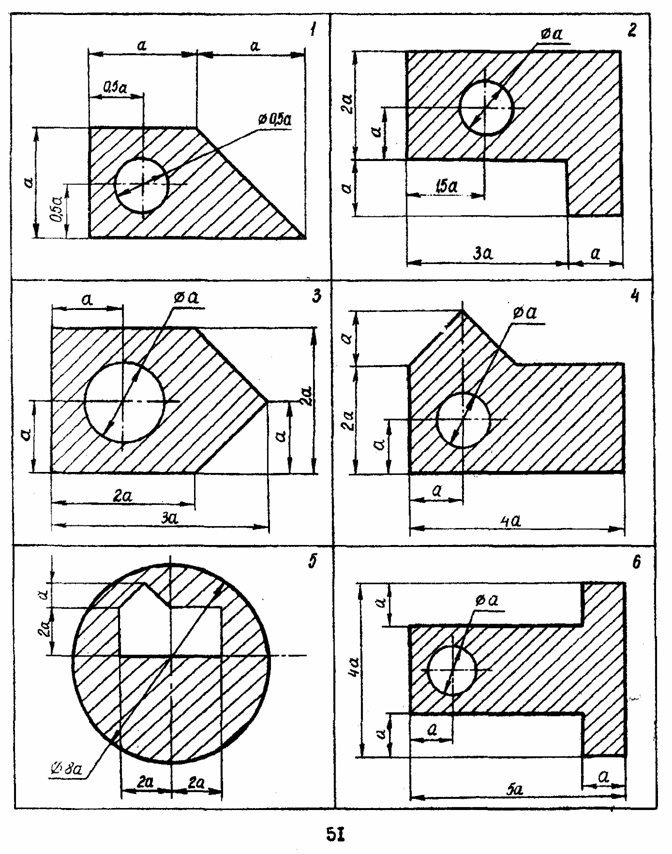
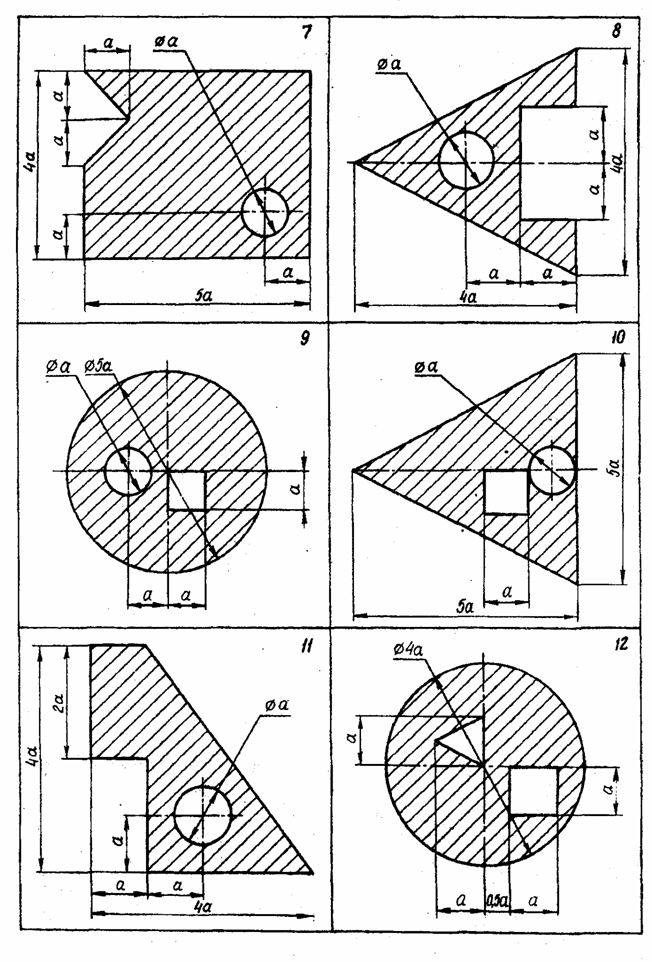
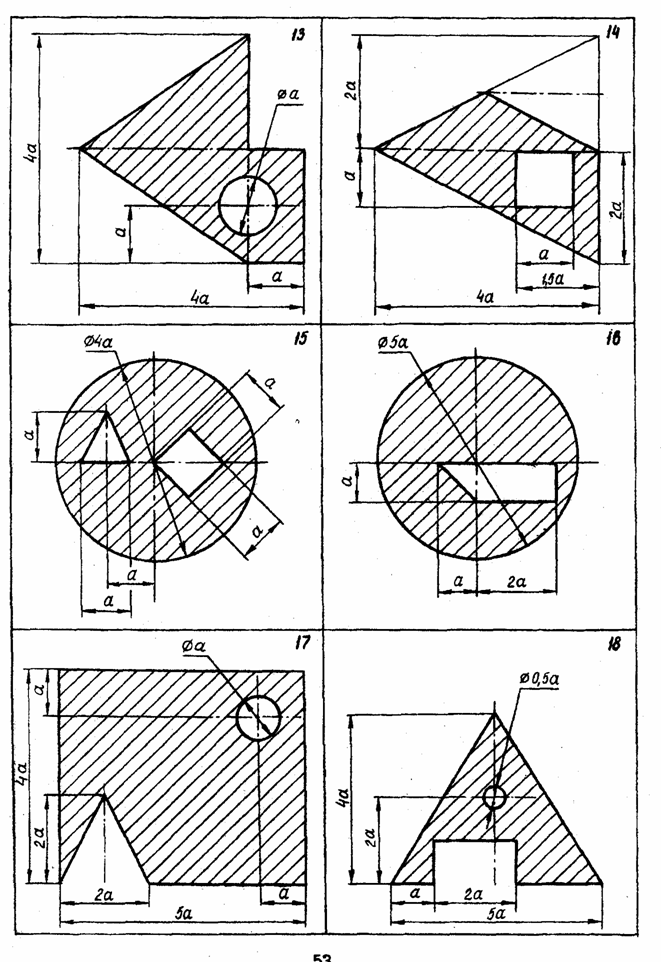
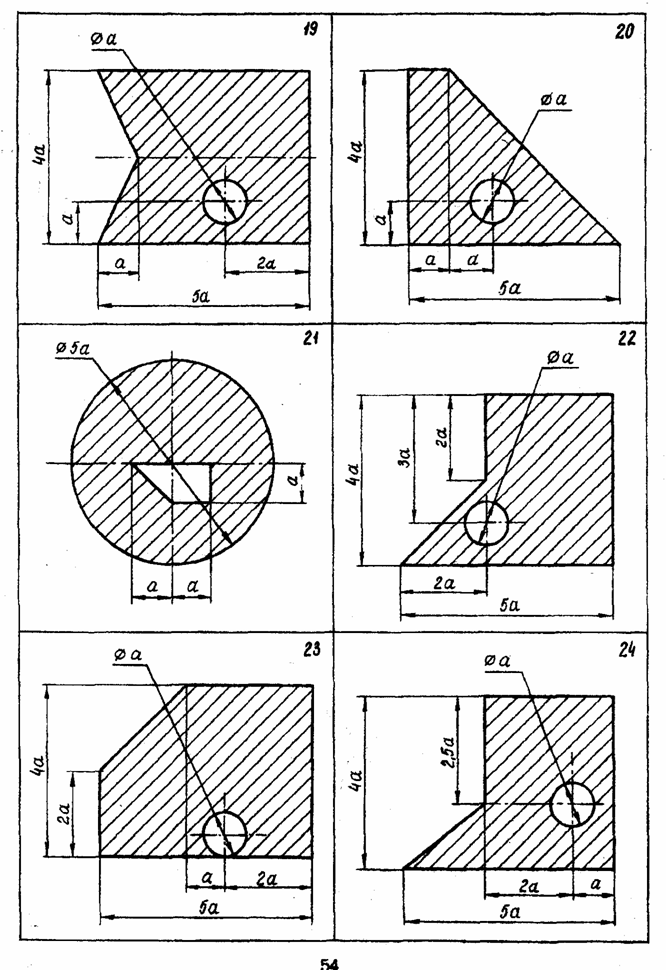
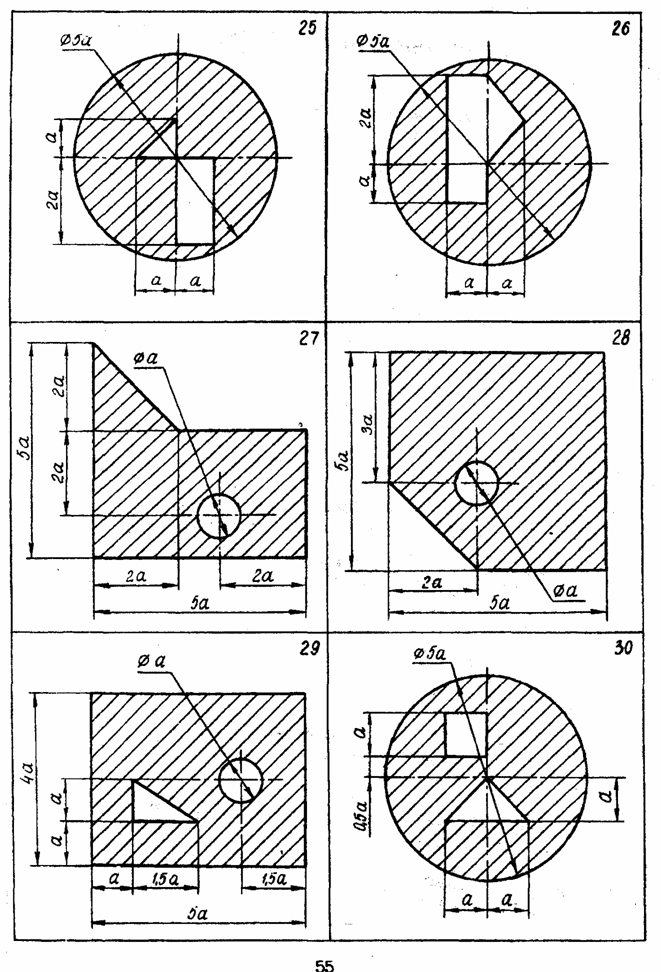
ЗАДАЧА 3 РАСЧЕТ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ

Рассчитать координаты центра тяжести заштрихованной части изображенной плоской фигуры относительно выбранной системы координат.

Таблица 3. Исходные данные к задаче 3

Методические указания к решению задачи 3

Расчет координат центра тяжести плоской фигуры.

Решение задач на определение центра тяжести плоской фигуры рекомендуется проводить в следующем порядке:

1. сложное сечение разбиваем на простые, положение центра тяжести которых известно, либо легко может быть определено;

2. выбираем произвольно координатные оси. Если плоская фигура имеет ось симметрии, то рекомендуется провести одну из координатных осей вдоль оси симметрии. Так как центр тяжести С сечения лежит на оси симметрии (т.е. на одной из координатных осей), то необходимо определить лишь одну координату;

3. определяем площади простых сечений;

4. определяем координаты центров тяжести простых сечений относительно выбранных осей координат. Координаты центров тяжести простейших фигур смотреть в конце данного раздела;

5. найденные значения подставляем в формулы:

где А1, А2 ... АК - площади простых сечений,

x1, x2 … xK,

y1, y2 … yК –  координаты центра тяжести простых сечений;

6. значения XC,YC откладываем от выбранных осей координат с учетом знака, т.е. от точки О в положительном направлении координаты со знаком «плюс» и в отрицательном направлении координаты со знаком «минус».